题目内容
16.给出下列命题:①命题:“?x0>0,sinx0≤x”的否定是:“?x>0,sinx>x”;
②函数f(x)=sinx+$\frac{2}{sinx}$(x∈(0,π))的最小值是2$\sqrt{2}$;
③在△ABC中,若sin2A=sin2B,则△ABC是等腰或直角三角形;
④设m,n为直线,α为平面,若m∥n,m∥α,则n∥α.
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①利用命题的否定定义即可判断正误;
②函数f(x)=sinx+$\frac{2}{sinx}$(x∈(0,π)),令sinx=t∈(0,1),则g(t)=t+$\frac{2}{t}$,利用导数研究其单调性极值,即可判断正误;
③在△ABC中,若sin2A=sin2B,则2A=2B或2A+2B=π,即可判断正误;
④由条件可得:n∥α或n?α,即可判断正误.
解答 解:①命题:“?x0>0,sinx0≤x”的否定是:“?x>0,sinx>x”,正确;
②函数f(x)=sinx+$\frac{2}{sinx}$(x∈(0,π)),令sinx=t∈(0,1],则g(t)=t+$\frac{2}{t}$,g′(t)=1-$\frac{2}{{t}^{2}}$<0,
因此函数g(t)在(0,1]单调递减,有最小值3,因此不正确;
③在△ABC中,若sin2A=sin2B,则2A=2B或2A+2B=π,因此△ABC是等腰或直角三角形,正确;
④设m,n为直线,α为平面,若m∥n,m∥α,则n∥α或n?α,因此不正确.
其中正确命题的个数是2.
故选:B.
点评 本题考查了简易逻辑的判定方法、利用导数研究函数的单调性与极值、解三角形、线面平行的判定定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知b为实数,i为虚数单位,若$\frac{2+b•i}{1-i}$为实数,则b=( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
11.若a,b,x∈R,a>b>1>x>0,则下列不等式成立的是( )
| A. | ax<bx | B. | xa>xb | C. | logxa>log${\;}_{{x}^{2}}$b | D. | logax>logbx |
1.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 2+$\sqrt{2}$+$\sqrt{6}$ | B. | 3+$\sqrt{2}$+$\sqrt{6}$ | C. | 2+$\sqrt{2}$+$\sqrt{3}$ | D. | 3+$\sqrt{2}$+$\sqrt{3}$ |
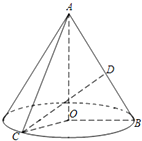 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.



 如图,正方体A1B1C1D1-ABCD中,E,F分别是AD,BC1的中点.
如图,正方体A1B1C1D1-ABCD中,E,F分别是AD,BC1的中点.