题目内容
19.甲、乙两人各进行一次射击,假设两人击中目标的概率分别是0.6和0.7,且射击结果相互独立,则甲、乙至多一人击中目标的概率为0.58.分析 根据题意可得两人是否击中目标是相互独立的,利用相互独立事件的概率乘法公式可得答案.
解答 解:由题意可得:两人是否击中目标是相互独立的,
因为两人击中目标的概率分别是0.6和0.7,
所以两人都击中目标的概率为:0.6×0.7=0.42,
所以甲、乙至多一人击中目标的概率为:1-0.42=0.58.
故答案为:0.58.
点评 本题主要考查相互独立事件的定义与相互独立事件的概率乘法公式的应用,此题属于基础题,只要学生认知细心的计算即可得到全分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知b为实数,i为虚数单位,若$\frac{2+b•i}{1-i}$为实数,则b=( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
11.若a,b,x∈R,a>b>1>x>0,则下列不等式成立的是( )
| A. | ax<bx | B. | xa>xb | C. | logxa>log${\;}_{{x}^{2}}$b | D. | logax>logbx |
8.已知函数f(x)=$\frac{2}{{e}^{x}+1}$+sinx(e为自然对数的底),则函数y=f(x)在区间[-$\frac{π}{3}$,$\frac{π}{3}$]上的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
9.若a是实数,则“a2≠4”是“a≠2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
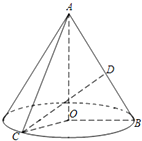 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.