题目内容
13.一个几何体的三视图如图所示,则该几何体的表面积为2$\sqrt{2}$π+2π+4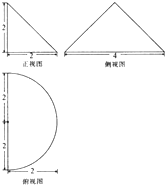
分析 根据几何体的三视图,得出该几何体是一底面为半圆,高为2的半圆锥,结合图中数据,求出它的表面积.
解答 解:根据几何体的三视图,得;
该几何体是一底面为半圆,高为2的半圆锥,
且底面半圆的半径为2;
∴该半圆锥的表面积为
S表面积=S半圆+S△+S侧面展开图
=$\frac{1}{2}$π•22+$\frac{1}{2}$×4×2+$\frac{1}{2}$×$\frac{1}{2}$×2π•2×$\sqrt{{2}^{2}{+2}^{2}}$
=2π+4+2$\sqrt{2}$π.
故答案为:2$\sqrt{2}$π+2π+4.
点评 本题考查了空间几何体的三视图的应用问题,解题时应根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.一个几何体的三视图如图所示,则该几何体的表面积为( )
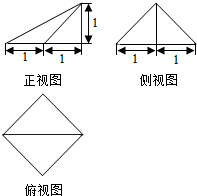

| A. | 2+$\sqrt{2}$+$\sqrt{6}$ | B. | 3+$\sqrt{2}$+$\sqrt{6}$ | C. | 2+$\sqrt{2}$+$\sqrt{3}$ | D. | 3+$\sqrt{2}$+$\sqrt{3}$ |
8.已知函数f(x)=$\frac{2}{{e}^{x}+1}$+sinx(e为自然对数的底),则函数y=f(x)在区间[-$\frac{π}{3}$,$\frac{π}{3}$]上的大致图象是( )
| A. |  | B. |  | C. | 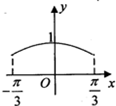 | D. | 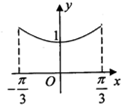 |
18.将函数f(x)=2sin(2x+$\frac{π}{4}$)的图象向右平移φ(φ>0)个单位,再将图象上每一点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),所得图象关于直线x=$\frac{π}{4}$对称,则φ的最小值为( )
| A. | $\frac{1}{8}π$ | B. | $\frac{1}{2}π$ | C. | $\frac{3}{4}π$ | D. | $\frac{3}{8}π$ |
2.执行如图所示程序框图,则输出a=( )
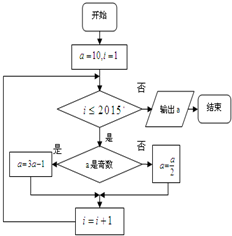

| A. | 20 | B. | 14 | C. | 10 | D. | 7 |
3.某农科院对春季昼夜温差大小与某早稻新品种发芽多少之间的关系进行分析研究,他们分别记录了2月1日至2月6日的每天昼夜温差与实验室每天200颗种子的发芽数,得到如下资料:
该农科院确定的研究方案是:先从这五组数据中取出2组,用剩下的4组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是2月3日与2月5日的两组数据,请根据余下四组数据,求出y对x的线性回归方程$\widehat{y}$=bx+a(精确到0.1);
(3)把取出的2组数据代入(2)中所求的回归方程,若|yi-$\widehat{{y}_{i}}$|(其中yi为i日的发芽数,$\widehat{{y}_{i}}$为i日根据(2)中回归方程得到的发芽数)的值都不大于2,则认为回归方程符合要求,问(2)中回归方程是否符合要求.
| 日期 | 2月1日 | 2月2日 | 2月3日 | 2月4日 | 2月5日 | 2月6日 |
| 温差x(℃) | 9 | 10 | 7 | 8 | 12 | 13 |
| 发芽数y(颗) | 23 | 26 | 17 | 21 | 27 | 30 |
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是2月3日与2月5日的两组数据,请根据余下四组数据,求出y对x的线性回归方程$\widehat{y}$=bx+a(精确到0.1);
(3)把取出的2组数据代入(2)中所求的回归方程,若|yi-$\widehat{{y}_{i}}$|(其中yi为i日的发芽数,$\widehat{{y}_{i}}$为i日根据(2)中回归方程得到的发芽数)的值都不大于2,则认为回归方程符合要求,问(2)中回归方程是否符合要求.
 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.