题目内容

3．求等差数列{an}中，a1=3，a4=9．
（1）求数列{an}的通项公式；
（2）若数列{an}的前n项和为Sn=80，求n的值．

分析 （1）由题意易得公差d的值，易得通项公式；
（2）由题意和前n项和公式易得n的方程，解方程可得n值．

解答 解：（1）∵等差数列{an}中，a1=3，a4=9，
∴公差d=$\frac{{a}_{4}-{a}_{1}}{4-1}$=2，
∴数列{an}的通项公式an=3+2（n-1）=2n+1；
（2）∵数列{an}的前n项和为Sn=80，
∴$\frac{n（3+2n+1）}{2}$=80，解得n=8
∴n的值为8

点评 本题考查等差数列的通项公式和求和公式，属基础题．

练习册系列答案
相关题目
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）离心率为$\frac{1}{2}$，长轴长为4．
（1）求椭圆标准方程；
（2）若直线l：y=kx+m与椭圆C交于A、B两点，S△AOB=$\sqrt{3}$，O为原点，kOA•kOB是否为定值，若为定值，求出该定值，若不是，说明理由．
14．已知圆C1的圆心在坐标原点O，且恰好与直线l1：x-2y+3$\sqrt{5}$=0相切，点A为圆上一动点，AM⊥x轴于点M，且动点N满足$\overrightarrow{ON}=\frac{2}{3}\overrightarrow{OA}+（{\frac{{2\sqrt{2}}}{3}-\frac{2}{3}}）\overrightarrow{OM}$，设动点N的轨迹为曲线C．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l与椭圆C相交于不同两点A，B，且满足$\overrightarrow{OA}⊥\overrightarrow{OB}$（O为坐标原点），求线段AB长度的取值范围．
11．对?x∈（0，$\frac{π}{2}$），下列四个命题：①sinx+tanx＞2x；②sinx•tanx＞x2；③sinx+tanx＞$\frac{8}{3}$x；④sinx•tanx＞2x2，则正确命题的序号是（　　）
A．①、②B．①、③C．③、④D．②、④
18．函数y=tan（$\frac{π}{4}x-\frac{π}{2}$）的部分图象如图所示，则△AOB的面积等于（　　）
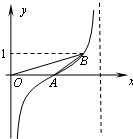
A．1B．2C．4D．$\frac{9}{2}$
8．已知正数a，b满足a+3b=5ab，实数x，y满足$\left\{\begin{array}{l}{x-y≤2}\\{x+2y≥5}\\{y-2≤0}\end{array}\right.$，若z=ax+by，求当3a+4b取最小值时z的最大值．
15．已知z为复数，（1-i）2z=（1+i）3（i为虚数单位），则$\overline z$=（　　）
A．1+iB．-1+iC．1-iD．-1-i
12．将函数f（x）=3sin（2x+θ）（-$\frac{π}{2}$＜θ＜$\frac{π}{2}$）的图象向右平移φ（φ＞0）个单位长度后得到函数g（x）的图象，若f（x），g（x）的图象都经过点P（0，$\frac{3\sqrt{2}}{2}$），则φ的值不可能是（　　）
A．$\frac{3π}{4}$B．πC．$\frac{5π}{4}$D．$\frac{7π}{4}$
13．教育部规定中学生每天体育锻炼不少于一个小时，各个学校认真执行，阳光体育正如火如荼．为了检查学校阳光体育开展情况，从学校随机抽取了20个人，由于项目较多和学生爱好原因，本次检查计算了每人篮球和羽毛球活动时间之和，以这个时间作为该同学的阳光体育活动时间．已知这20个人的阳光体育活动时间都在3小时到8小时之间，并绘制出如图的频率分布直方图．
（Ⅰ）求x的值，并求一周内阳光体育活动时间在[6，8]小时的人数；
（Ⅱ）从阳光体育时间在[6，8]小时的同学中抽取2人，求恰有1人的阳光体育活动时间在[6，7）小时的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网