题目内容
8.下列说法正确的是( )| A. | 已知p:?x0∈R,x02+x0-1=0,q:?x∈R,x2+x+1>0,则p∧q是真命题 | |
| B. | 命题p:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b=0$的否命题是:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b≠0$ | |
| C. | ?x∈R,x2+x-1<0的否定是?x0∈R,x02+x0-1>0 | |
| D. | x=$\frac{π}{3}$是$y=sin(2x-\frac{π}{6})$取最大值的充要条件 |
分析 A.p:由于△>0,因此方程有实数根,p是真命题,q:由x2+x+1=$(x+\frac{1}{2})^{2}+\frac{3}{4}$>0,是真命题,即可判断出p∧q的真假;
B.利用否命题的定义即可判断出正误;
C.利用命题的否定即可判断出正误;
D.例如x=$\frac{π}{3}$+π时函数也可以取得最大值,即可判断出正误.
解答 解:A.p:?x0∈R,x02+x0-1=0,由于△>0,因此方程有实数根,是真命题,q:?x∈R,x2+x+1=$(x+\frac{1}{2})^{2}+\frac{3}{4}$>0,是真命题,因此p∧q是真命题,正确;
B.命题p:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b=0$的否命题是:若$\overrightarrow{a}$与$\overrightarrow{b}$不垂直,则$\overrightarrow a•\overrightarrow b≠0$,不正确;
C.?x∈R,x2+x-1<0的否定是?x0∈R,x02+x0-1≥0,因此不正确;
D.x=$\frac{π}{3}$是$y=sin(2x-\frac{π}{6})$取最大值的充分不必要条件,例如x=$\frac{π}{3}$+π时也可以取得最大值,因此不正确.
故选:A.
点评 本题考查了简易逻辑的判定方法、三角函数的性质、一元二次方程的解与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.函数y=tan($\frac{π}{4}x-\frac{π}{2}$)的部分图象如图所示,则△AOB的面积等于( )
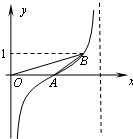

| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{9}{2}$ |
16.487被7除的余数为a(0≤a<7),则${(x-\frac{a}{x^2})^6}$展开式中x-3的系数为( )
| A. | 4320 | B. | -4320 | C. | 20 | D. | -20 |
18.设全集U=R,集合M={x|y=lg(x2-1)},N={0<x<2},则(CUM)∩N=( )
| A. | {x|-2≤x≤1} | B. | {x|0<x≤1} | C. | {x|0<x<2} | D. | {x|x<R} |
 教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.
教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.