题目内容
【题目】已知数列{an}的前n项和为Sn , 若4Sn=(2n﹣1)an+1+1,且a1=1.
(1)求数列{an}的通项公式;
(2)设cn= ![]() ,数列{cn}的前n项和为Tn .
,数列{cn}的前n项和为Tn .
①求Tn;
②对于任意的n∈N*及x∈R,不等式kx2﹣6kx+k+7+3Tn>0恒成立,求实数k的取值范围.
【答案】
(1)解:∵4Sn=(2n﹣1)an+1+1,
∴4Sn﹣1=(2n﹣3)an+1,n≥2
∴4an=(2n﹣1)an+1﹣(2n﹣3)an,
整理得(2n+1)an=(2n﹣1)an+1,
即 ![]() =
= ![]() ,
,
∴ ![]() =3,
=3, ![]() =
= ![]() ,…,
,…, ![]() =
= ![]()
以上各式相乘得 ![]() =2n﹣1,又a1=1,
=2n﹣1,又a1=1,
所以an=2n﹣1,
(2)解:①∵cn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴Tn= ![]() (1﹣
(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )=
)= ![]() (1﹣
(1﹣ ![]() )=
)= ![]() ,
,
②由①可知Tn= ![]() ,
,
∴ ![]() ≥
≥ ![]() ,
,
∵kx2﹣6kx+k+7+3Tn>0恒成立,
∴kx2﹣6kx+k+8>0恒成立,
当k=0时,8>0恒成立,
当k≠0时,则得 ![]() ,解得0<k<1,
,解得0<k<1,
综上所述实数k的取值范围为[0,1)
【解析】(1)充分利用已知4Sn=(2n﹣1)an+1+1,将式子中n换成n﹣1,然后相减得到an与an+1的关系,利用累乘法得到数列的通项,(2)①利用裂项求和,即可求出Tn ,
②根据函数的思想求出 ![]() ≥
≥ ![]() ,问题转化为kx2﹣6kx+k+8>0恒成立,分类讨论即可.
,问题转化为kx2﹣6kx+k+8>0恒成立,分类讨论即可.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系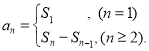 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

练习册系列答案
相关题目