题目内容
已知抛物线的方程是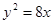 ,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲
,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲
线的标准方程是 ______,其渐近线方程是______________
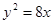 ,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲
,双曲线的右焦点是抛物线的焦点,离心率为2,则双曲线的标准方程是 ______,其渐近线方程是______________
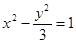 ,
, 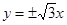
分析:先根据抛物线方程求得焦点坐标,进而确定双曲线的顶点,求得双曲线中的a,根据离心率进而求c,最后根据b2=c2-a2求得b,则双曲线的方程及其渐近线方程可得.
解:由题可设双曲线的方程为:
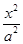 -
-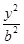 =1.
=1.∵抛物线y2=8x中2p=8,
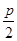 =2,
=2,∴其焦点F(2,0),
又因为双曲线的右焦点是抛物线的焦点,
则有:c=2,又e=
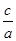 =2
=2∴a=1,故b2=c2-a2=4-1=3,
双曲线的方程为 x2-
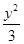 =1.
=1.其渐近线方程是 y=±
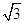 x
x故答案为:x2-
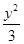 =1;y=±
=1;y=±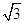 x.
x.
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
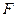 是椭圆
是椭圆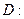
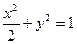 的右焦点,过点
的右焦点,过点 且斜率为
且斜率为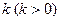 的直线
的直线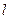 与
与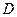 交于
交于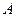 、
、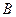 两点,
两点,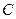 是点
是点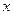 轴的对称点.
轴的对称点.
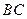 上;
上;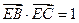 ,求
,求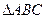 外接圆的方程.
外接圆的方程.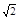
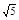
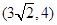 到两焦点的距离之和是12,则椭圆的标准方程是 .
到两焦点的距离之和是12,则椭圆的标准方程是 .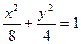 的左右焦点为
的左右焦点为 ;直线
;直线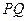 经过
经过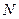 交椭圆于
交椭圆于 两点.
两点.
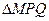 的周长为定值.
的周长为定值.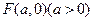 ,动点
,动点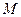 、
、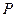 分别在
分别在 、
、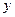 轴上运动,满足
轴上运动,满足 ,
,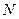 为动点,并且满足
为动点,并且满足 .
.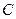 的方程;
的方程;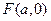 的直线
的直线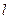 (不与
(不与 两点,设点
两点,设点 ,
,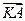 与
与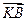 的夹角为
的夹角为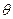 ,求证:
,求证: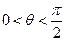 .
.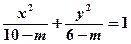 与曲线
与曲线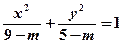 具有相同的焦距,则
具有相同的焦距,则 的取值范围是
的取值范围是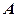 .
.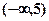
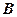 .
.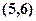
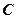 .
.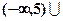
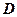 .
.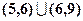
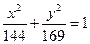 有共同焦点,且过点
有共同焦点,且过点 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。