题目内容
已知椭圆的中心在坐标原点，焦点在x轴上，椭圆上点P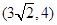
到两焦点的距离之和是12，则椭圆的标准方程是 ．
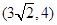到两焦点的距离之和是12，则椭圆的标准方程是 ．
+
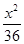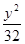=1分析：由题设条件知2a=12，则a=6，可设椭圆的标准方程是：
+
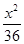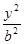=1，将点P的坐标代入进而可得b，由此可知所求椭圆方程．解：由题设知，2a=12，
∴a=6，
可设椭圆的标准方程是：
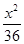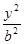+=1，b2=32，∴所求椭圆方程为
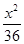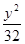+=1．故答案为：
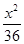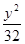+=1．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
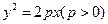的焦点为
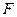，过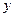
轴正半轴于点
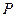，交抛物线于
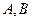两点，其中点
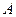在第一象限.
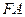为直径的圆与
,
,
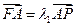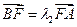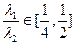，求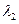
的取值范围.
的焦点，过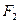
作垂直于
轴的直线交双曲线与点P且∠P F1F2=300，求双曲线的渐近线方程。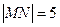
，点P是线段MN上一点，且
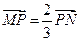，点P随线段MN的运动而变化.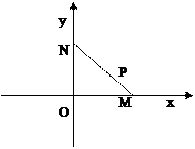
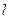，与曲线C交于A．B两点，O是坐标原点，设
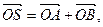是否存在这样的直线
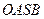的对角线相等（即
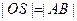）？若存在，求出直线
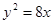，双曲线的右焦点是抛物线的焦点，离心率为2，则双曲
. 
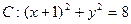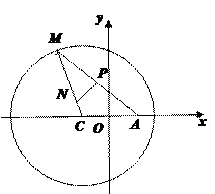
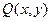是圆C上一点，求
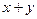的取值范围；
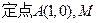为圆C上一动点，点P在AM上，点N在CM上，且满足
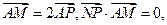求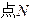
的轨迹的内接矩形的最大面积.
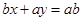的距离等于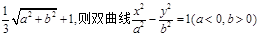
的半焦距的最小值为 （ ）
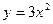与直线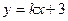
的交点为（2，b），则
=" " ，
=" " 
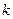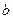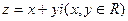满足
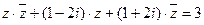.求复数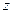
在复平面上对应点的轨迹.