题目内容
5.在等差数列{an}中,a1=7,公差d$∈(-1,-\frac{7}{8})$,则其前n项和Sn的最大值为( )| A. | S6 | B. | S7 | C. | S8 | D. | S9 |
分析 由题意可得Sn的表达式,由二次函数的性质可得.
解答 解:由题意可得Sn=7n+$\frac{n(n-1)}{2}$d=$\frac{d}{2}$n2+(7-$\frac{d}{2}$)n,
可得关于n的二次函数开口向下,
对称轴为n=$-\frac{7-\frac{d}{2}}{2×\frac{d}{2}}$=$\frac{1}{2}$-$\frac{7}{d}$,
∵d$∈(-1,-\frac{7}{8})$,∴$\frac{7}{d}$∈(-8,-7),
∴$\frac{1}{2}$-$\frac{7}{d}$∈($\frac{15}{2}$,$\frac{17}{2}$),
∵n为正整数,∴n=8
故选:C
点评 本题考查等差数列的求和公式,涉及二次函数的最值,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知数列{an}满足a1=2,an+1=$\frac{{1+{a_n}}}{{1-{a_n}}}$,则a15等于( )
| A. | 2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{3}$ |
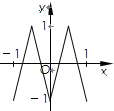
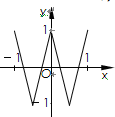
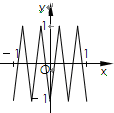
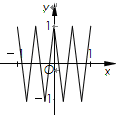
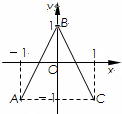 如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )