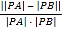题目内容
【题目】已知函数![]() ,若关于
,若关于![]() 的方程
的方程![]() 有四个不相等的实数根,则实数
有四个不相等的实数根,则实数![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】
方程![]() 有四个不相等的实数根,即方程
有四个不相等的实数根,即方程![]() 有四个不相等的实数根,则
有四个不相等的实数根,则![]() 或
或![]() 有四个不相等的实数根,结合图象利用分类讨论
有四个不相等的实数根,结合图象利用分类讨论![]() 与
与![]() 的根的情况,其中当
的根的情况,其中当![]() 时分别构造函数
时分别构造函数![]() 与
与![]() 分析,最后由转化思想将函数
分析,最后由转化思想将函数![]() 有两个零点转化为
有两个零点转化为![]() 小于0构造不等式求得答案.
小于0构造不等式求得答案.
方程![]() 有四个不相等的实数根,即方程
有四个不相等的实数根,即方程![]() 有四个不相等的实数根,则
有四个不相等的实数根,则![]() 或
或![]() 有四个不相等的实数根,
有四个不相等的实数根,
因为函数![]() ,
,
对方程![]() 的根分析,令
的根分析,令![]() ,
,
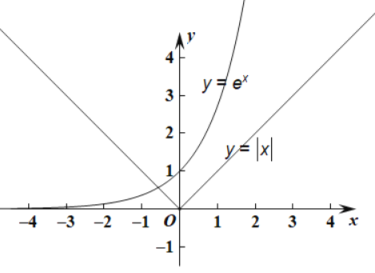
由图象分析可知,当![]() 时,必有一根,
时,必有一根,
当![]() 时,令
时,令![]() ,则
,则![]() ,所以函数
,所以函数![]() 单调递增,故
单调递增,故![]() ,所以当
,所以当![]() 时,方程
时,方程![]() 无根,
无根,
故方程![]() 只有1个根,那么方程
只有1个根,那么方程![]() 应有3个根,
应有3个根,
对方程![]() 的根分析,令
的根分析,令![]() ,
,
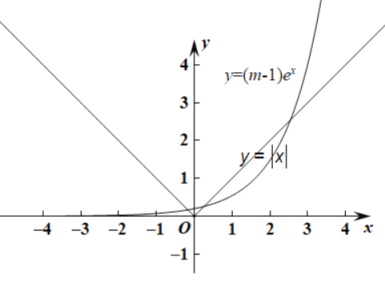
由图象分析可知,当![]() 时,必有一根,
时,必有一根,
当![]() 时,方程
时,方程![]() 应有2两个不等的实根,其等价于方程
应有2两个不等的实根,其等价于方程![]() 有2个不等的实根,
有2个不等的实根,
令![]() ,则
,则![]() ,且其在
,且其在![]() 内有两个零点,
内有两个零点,
显然当![]() ,函数
,函数![]() 单调递增,不满足条件,则
单调递增,不满足条件,则![]() ;
;
令![]() ,则函数
,则函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间 ![]() 单调递增;
单调递增;
所以函数![]() 在
在![]() 取得极小值,同时也为最小值,
取得极小值,同时也为最小值,![]() ,
,
函数![]() 若要有两个零点,则
若要有两个零点,则![]() ,
,
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]()

【题目】某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
(1)在甲组内任选两人,求恰有一人优秀的概率;
(2)每个员工技能测试是否达标相互独立,以频率作为概率.
(i)设公司员工在方式一、二下的受训时间分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
(ii)按(i)中所选方式从公司任选两人,求恰有一人优秀的概率.
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()