题目内容
【题目】某公司培训员工某项技能，培训有如下两种方式，方式一：周一到周五每天培训1小时，周日测试；方式二：周六一天培训4小时，周日测试．公司有多个班组，每个班组60人，现任选两组(记为甲组、乙组)先培训，甲组选方式一，乙组选方式二，并记录每周培训后测试达标的人数如下表，其中第一、二周达标的员工评为优秀．
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
（1）在甲组内任选两人，求恰有一人优秀的概率；
（2）每个员工技能测试是否达标相互独立，以频率作为概率.
（i）设公司员工在方式一、二下的受训时间分别为
、
，求、的分布列，若选平均受训时间少的，则公司应选哪种培训方式？
（ii）按（i）中所选方式从公司任选两人，求恰有一人优秀的概率．
【答案】（1）
（2）（i）见解析（ii）
【解析】
（1）甲组
人中有
人优秀，利用超几何分布概率计算公式，计算得“甲组内任选两人，求恰有一人优秀的概率”.（2）
可能取值有
，根据题目所给数据计算出每种取值对应的频率也即概率，由此得到分布列并其算出期望值.
的所有可能取值为
，根据题目所给数据计算出每种取值对应的频率也即概率，由此得到分布列并其算出期望值.根据两个期望值较小的即为选择.（3）先计算出从公司任选一人，优秀率为
，再按照二项分布的概率计算公式计算得“从公司任选两人，求恰有一人优秀的概率”
解：（1）甲组60人中有45人优秀，任选两人，
恰有一人优秀的概率为
；
（2）（i）的分布列为
| 5 | 10 | 15 | 20 |
P |
|
|
|
|
，
的分布列为
| 4 | 8 | 12 | 16 |
P |
|
|
|
|
，
∵
，∴公司应选培训方式一；
（ii）按培训方式一，从公司任选一人，其优秀的概率为
，
则从公司任选两人，恰有一人优秀的概率为
．
阅读快车系列答案
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：
（1）记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
【题目】某工厂生产某种型号的农机具零配件，为了预测今年7月份该型号农机具零配件的市场需求量，以合理安排生产，工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查，销售单价
（单位：元）和销售量
（单位：千件）之间的6组数据如下表所示：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
（1）根据1至6月份的数据，求关于的线性回归方程（系数精确到0.01）；
（2）结合（1）中的线性回归方程，假设该型号农机具零配件的生产成本为每件3元，那么工厂如何制定7月份的销售单价，才能使该月利润达到最大？（计算结果精确到0.1）
参考公式：回归直线方程
，
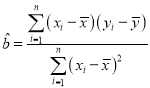
参考数据：
，
