题目内容

3．画出下列方程所表示的曲线．
（1）（x-2）2+（y+7）2=0；
（2）（x-1）2=8-（y+2）2；
（3）y=$\sqrt{2-{x}^{2}}$．

分析 利用所给方程，即可画出方程所表示的曲线．

解答 解：（1）（x-2）2+（y+7）2=0，表示点（2，-7）；

（2）（x-1）2=8-（y+2）2，表示以（1．-2）为圆心，2$\sqrt{2}$为半径的圆；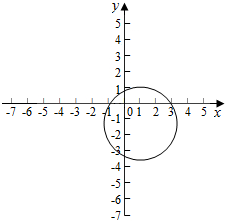

（3）y=$\sqrt{2-{x}^{2}}$，表示以原点为圆心，$\sqrt{2}$为半径的圆的上半圆．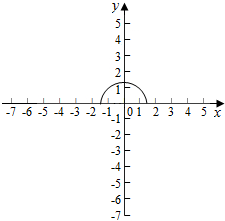

点评 本题考查圆的方程与图象，考查学生的作图能力，比较基础．

练习册系列答案
相关题目
13．如图是一个算法的程序框图，若输入的x的值为2，则输出的y的值是（　　）
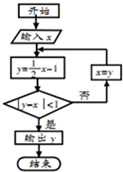
A．0B．-1C．-$\frac{3}{2}$D．-$\frac{7}{4}$
14．已知实数x，y满足x2+y2-xy+2x-y+1=0，求x，y的值．
11．已知f（f（f（x）））=27x+13，求函数f（x）的解析式f（x）=3x+1．
18．已知函数f（x）对任意实数a、b，都有f（ab）=f（a）+f（b）成立．
（1）求f（0）与f（1）的值；
（2）求证：f（$\frac{1}{x}$）=-f（x）；
（3）若f（2）=p，f（3）=q（p，q均为常数），求f（36）的值．
8．若圆C1：x2+y2=16与圆C2：（x-a）2+y2=1相切．则a的值为（　　）
A．±3B．±5C．3或5D．±3或±5
15．设函数f（x）=$\left\{\begin{array}{l}{-x-1，x≤0}\\{\sqrt{x}，x＞0}\end{array}\right.$，若f（x0）＞1．则x0的取值范围是（-∞，-2）∪（1，∞）．
12．已知函数f（x）=3x2-5x+2，求f（-$\sqrt{2}$），f（-a），f（a+3），f（a）
15．已知集合A={x|$\frac{π}{4}$≤x≤$\frac{π}{2}$}，函数f（x）=4sin2（$\frac{π}{4}$+x）-2$\sqrt{3}$cos2x-1，x∈A，求f（x）的最大值及最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网