题目内容
【题目】试比较3－
与
（n为正整数）的大小，并予以证明．
【答案】见解析
【解析】
利用作差法可得3－
－
＝
，确定3－与的大小关系等价于比较
与2n＋1的大小，利用数学归纳法证明即可.
证明：3－－＝，
于是确定3－与的大小关系等价于比较与2n＋1的大小．
由2＜2×1＋1，
＜2×2＋1，
＞2×3＋1，
＞2×4＋1，
＞2×5＋1，
可猜想当n≥3时，＞2n＋1，
证明如下：
ⅰ当n＝3时，由上可知显然成立．
ⅱ假设当n＝k时，
＞2k＋1成立．
那么，当n＝k＋1时，
＝2×＞2(2k＋1)＝4k＋2＝2(k＋1)＋1＋(2k－1)＞2(k＋1)＋1，
所以当n＝k＋1时猜想也成立，
综合ⅰ和ⅱ，对一切n≥3的正整数，都有＞2n＋1．
所以当n＝1，2时，3－＜；
当n≥3时，3－＞（n为正整数）．
练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y＝﹣x2+2|x|+1的图象和性质进行了探究，探究过程如下，请补充完整．
（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中，m＝ ．
（2）根据上表数据，在如图所示的平面直角坐标系中描点，画出了函数图象的一部分，请画出该函数图象的另一部分．
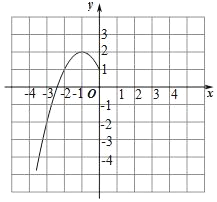
（3）观察函数图象，写出两条函数的性质．/p>
（4）进一步探究函数图象发现：
①方程﹣x2+2|x|+1＝0有 个实数根；
②关于x的方程﹣x2+2|x|+1＝a有4个实数根时，a的取值范围是 ．
