题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(2)当![]() 时,求函数
时,求函数![]() 的最大值及最小值.
的最大值及最小值.
【答案】(1)周期![]() ,增区间为
,增区间为![]() (2)最大值为
(2)最大值为![]() ,最小值为-1
,最小值为-1
【解析】
(1)找出函数f(x)解析式中的ω的值,代入周期公式即可求出函数的最小正周期,由正弦函数的单调递增区间[2kπ![]() ,2kπ
,2kπ![]() ]列出关于x的不等式,求出不等式的解集即为函数的单调递增区间;
]列出关于x的不等式,求出不等式的解集即为函数的单调递增区间;
(2)由x的范围,求出2x![]() 的范围,根据正弦函数的图象与性质可得2x
的范围,根据正弦函数的图象与性质可得2x![]() 为
为![]() 时,f(x)取得最大值,当2x
时,f(x)取得最大值,当2x![]() 为
为![]() 时函数f(x)取得最小值,分别求出最大值和最小值即可.
时函数f(x)取得最小值,分别求出最大值和最小值即可.
(1)f(x)![]() sin(2x
sin(2x![]() ),
),
∵ω=2,∴最小正周期T![]() π,由2kπ
π,由2kπ![]() 2x
2x![]() 2kπ
2kπ![]() (k∈Z),
(k∈Z),
解得kπ![]() x≤kπ
x≤kπ![]() (k∈Z),
(k∈Z),
故函数f(x)的单调增区间是[kπ![]() ,kπ
,kπ![]() ](k∈Z);
](k∈Z);
(2)当x∈[![]() ,
,![]() ]时,(2x
]时,(2x![]() )∈[
)∈[![]() ,
,![]() ],
],
故当2x![]() ,即x
,即x![]() 时,f(x)有最大值
时,f(x)有最大值![]() ,
,
当2x![]() ,即x
,即x![]() 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.

练习册系列答案
相关题目
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: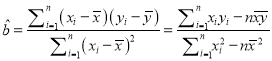 ,
, ![]() .
.
