题目内容
【题目】椭圆C： 
的左、右焦点分别是F1、F2，离心率为
，过F1且垂直于x轴的直线被椭圆C截得的线段长为l．
（1）求椭圆C的方程；
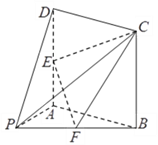
（2）点P是椭圆C上除长轴端点外的任一点，连接PF1、PF2，设∠F1PF2的角平分线PM交C的长轴于点M（m，0），求m的取值范围．
（3）在（2）的条件下，过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点．设直线PF1、PF2的斜率分别为k1、k2，若k≠0，试证明
为定值，并求出这个定值．
【答案】（1）
；（2）
；（3）-8
【解析】试题（1）根据题意可得
又因为
，所以可得a，b的值，即可得方程；（2）设出点p坐标，由两点式列出直线
方程，然后利用点m到两直线的距离相等来确定m值，再根据p点，横坐标的范围，来确定m范围；（3）设直线方程为
与椭圆方程联立，需满足
求得
，由（2）可知
，代入化简即可
试题解析：（1）由于
由题意知
又
（2）设
由题意知
由于点P在椭圆上，所以
所以
（3）设
则直线l的方程为
联立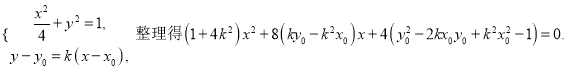
由题意得
又
由（2）知
所以
因此
黄冈天天练口算题卡系列答案
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数x（个） | 2 | 3 | 4 | 5 |
加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（1）求出y关于x的线性回归方程
；
（2）试预测加工10个零件需要多少小时？
（注：
=
，
=
-b
）
【题目】下表为北京市居民用水阶梯水价表(单位：元/立方米).
阶梯 | 户年用水量 （立方米） | 水价 | 其中 | ||
自来水费 | 水资源费 | 污水处理费 | |||
第一阶梯 | 0-180（含） | 5.00 | 2.07 | 1.57 | 1.36 |
第二阶梯 | 181-260（含） | 7.00 | 4.07 | ||
第三阶梯 | 260以上 | 9.00 | 6.07 | ||
（Ⅰ）试写出水费
(元)与用水量
(立方米)之间的函数关系式；
（Ⅱ）若某户居民年交水费1040元，求其中自来水费、水资源费及污水处理费各是多少？
