题目内容
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() 分别是线段
分别是线段![]() 的中点,
的中点,![]() .
.
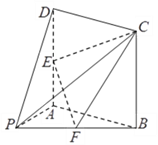
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,易得四边形
,易得四边形![]() 为平行四边形,从而
为平行四边形,从而![]()
所以![]() ∥平面
∥平面![]() ;(2)
;(2)![]() 平面
平面![]() ,且四边形
,且四边形![]() 是正方形,
是正方形,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求出平面
,求出平面![]() 与平面
与平面![]() 的法向量,代入公式得到所成锐二面角的余弦值.
的法向量,代入公式得到所成锐二面角的余弦值.
试题解析:
(1)取![]() 中点
中点![]() ,连接
,连接![]()
![]() 分别是
分别是![]() 中点,
中点, ![]() ,
,
![]() 为
为![]() 中点,
中点,![]() 为矩形,
为矩形,![]() ,
,
![]() ,
,![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
(2)![]() 平面
平面![]() ,且四边形
,且四边形![]() 是正方形,
是正方形,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]()
则![]()
![]()
![]()
设平面![]() 法向量为
法向量为![]() ,
,![]() ,
,![]()
则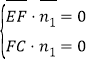 , 即
, 即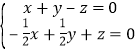 ,取
,取![]()
则设平面![]() 法向量为
法向量为![]() ,
,![]() ,
,![]()
则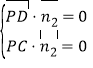 , 即
, 即![]() , 取
, 取![]()
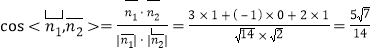 .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.