题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为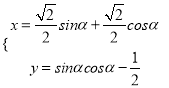 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析:(1)先根据三角函数平方关系消参数得曲线![]() 的普通方程,注意参数对自变量范围的限制,再根据
的普通方程,注意参数对自变量范围的限制,再根据![]() 将曲线
将曲线![]() 的极坐标方程化为直角坐标方程;(2)联立直线方程与抛物线段方程,求出相切时以及过端点时
的极坐标方程化为直角坐标方程;(2)联立直线方程与抛物线段方程,求出相切时以及过端点时![]() 的取值,结合图像确定
的取值,结合图像确定![]() 的取值范围.
的取值范围.
试题解析:解:(Ⅰ)因为![]() ,所以
,所以![]() .
.
由![]()
平方得: ![]()
又![]()
两式相减得![]() ,
,
故曲线![]() 的普通方程为
的普通方程为![]() ,
, ![]() .
.
另由![]() 得
得![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
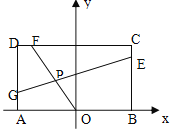
(Ⅱ)如图,当直线![]() 过点
过点![]() 时,
时, ![]() ;
;
当直线![]() 与
与![]() 相切时,
相切时,
由![]() 得
得![]()
由![]() 得
得![]() ,
,
从而,曲线![]() 与曲线
与曲线![]() 有公共点时,
有公共点时, ![]() .
.

练习册系列答案
相关题目
【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如下表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:![]() (
(![]() ).
).
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.