题目内容
建造一个容积为16立方米、深为4米的长方形无盖水池,如果池底和池壁的造价每平方米分别为60元和40元.请你设计一个方案,使水池的造价最低,最低造价是多少元?
设池底长为x米,宽为y米,水池的造价为L,则xy=4
∵池底和池壁的造价每平方米分别为60元和40元,
∴L=4×60+(2x+2y)×4×40=240+320(x+y)≥240+320×2
=1520,
当且仅当x=y=2时,L取得最小值1520元.
答:当池底长为2米,宽为2米时,水池的造价最低,最低造价是1520元.
∵池底和池壁的造价每平方米分别为60元和40元,
∴L=4×60+(2x+2y)×4×40=240+320(x+y)≥240+320×2
| xy |
当且仅当x=y=2时,L取得最小值1520元.
答:当池底长为2米,宽为2米时,水池的造价最低,最低造价是1520元.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
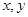 满足约束条件
满足约束条件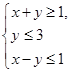 ,若
,若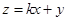 的最大值为
的最大值为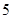 ,则实数
,则实数 .
.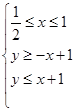 ,则
,则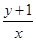 的最大值为________.
的最大值为________. 满足约束条件
满足约束条件 ,当目标函数
,当目标函数 在该约束条件下取到最小值
在该约束条件下取到最小值 时,
时, 的最小值为( )
的最小值为( )