题目内容
设 ,函数
,函数
 .
.
试讨论函数 的单调性.
的单调性.
 ,函数
,函数
 .
.试讨论函数
 的单调性.
的单调性.①当k=0时,F(x)在区间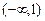 上单调递增,F(x)在区间
上单调递增,F(x)在区间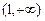 上单调递减;
上单调递减;
②当k<0时,F(x)在区间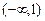 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间
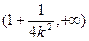 上单调递增;③当
上单调递增;③当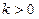 时,F(x)在区间
时,F(x)在区间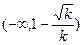 上单调递减,在区间
上单调递减,在区间
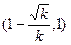 上单调递增,在区间
上单调递增,在区间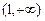 上单调递减.
上单调递减.
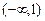 上单调递增,F(x)在区间
上单调递增,F(x)在区间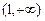 上单调递减;
上单调递减;②当k<0时,F(x)在区间
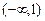 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间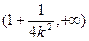 上单调递增;③当
上单调递增;③当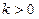 时,F(x)在区间
时,F(x)在区间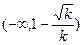 上单调递减,在区间
上单调递减,在区间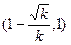 上单调递增,在区间
上单调递增,在区间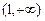 上单调递减.
上单调递减.分段函数要分段处理,由于每一段都是基本初等函数的复合函数,所以应该用导数来研究。
因为 ,所以
,所以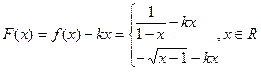 .
.
(1)当x<1时,1-x>0,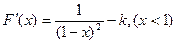
①当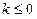 时,
时,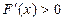 在
在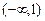 上恒成立,故F(x)在区间
上恒成立,故F(x)在区间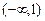 上单调递增;
上单调递增;
②当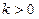 时,令
时,令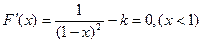 ,解得
,解得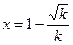 ,
,
且当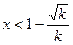 时,
时,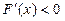 ;当
;当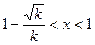 时,
时,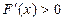
故F(x)在区间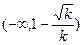 上单调递减,在区间
上单调递减,在区间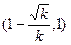 上单调递增;
上单调递增;
(2)当x>1时, x-1>0,
①当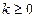 时,
时,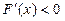 在
在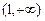 上恒成立,故F(x)在区间
上恒成立,故F(x)在区间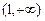 上单调递减;
上单调递减;
②当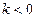 时,令
时,令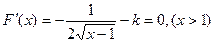 ,解得
,解得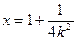 ,
,
且当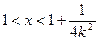 时,
时,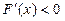 ;当
;当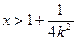 时,
时,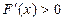
故F(x)在区间 上单调递减,在区间
上单调递减,在区间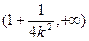 上单调递增;
上单调递增;
综上得,①当k=0时,F(x)在区间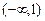 上单调递增,F(x)在区间
上单调递增,F(x)在区间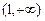 上单调递减;
上单调递减;
②当k<0时,F(x)在区间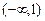 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间
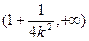 上单调递增;③当
上单调递增;③当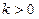 时,F(x)在区间
时,F(x)在区间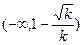 上单调递减,在区间
上单调递减,在区间
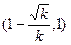 上单调递增,在区间
上单调递增,在区间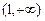 上单调递减.
上单调递减.
因为
 ,所以
,所以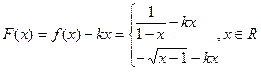 .
.(1)当x<1时,1-x>0,
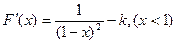
①当
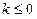 时,
时,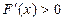 在
在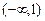 上恒成立,故F(x)在区间
上恒成立,故F(x)在区间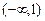 上单调递增;
上单调递增;②当
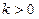 时,令
时,令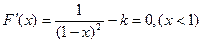 ,解得
,解得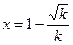 ,
,且当
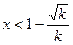 时,
时,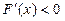 ;当
;当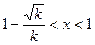 时,
时,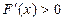
故F(x)在区间
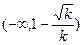 上单调递减,在区间
上单调递减,在区间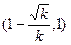 上单调递增;
上单调递增;(2)当x>1时, x-1>0,

①当
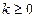 时,
时,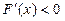 在
在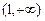 上恒成立,故F(x)在区间
上恒成立,故F(x)在区间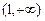 上单调递减;
上单调递减;②当
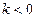 时,令
时,令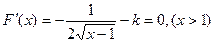 ,解得
,解得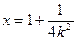 ,
,且当
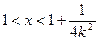 时,
时,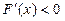 ;当
;当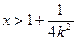 时,
时,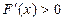
故F(x)在区间
 上单调递减,在区间
上单调递减,在区间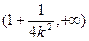 上单调递增;
上单调递增;综上得,①当k=0时,F(x)在区间
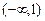 上单调递增,F(x)在区间
上单调递增,F(x)在区间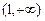 上单调递减;
上单调递减;②当k<0时,F(x)在区间
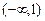 上单调递增,在区间
上单调递增,在区间 上单调递减,在区间
上单调递减,在区间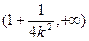 上单调递增;③当
上单调递增;③当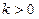 时,F(x)在区间
时,F(x)在区间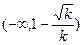 上单调递减,在区间
上单调递减,在区间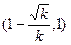 上单调递增,在区间
上单调递增,在区间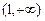 上单调递减.
上单调递减.
练习册系列答案
相关题目
 –(2a)2]对任意x∈[
–(2a)2]对任意x∈[ ,+∞]都有意义,则实数a的取值范围是( )
,+∞]都有意义,则实数a的取值范围是( )


 )
)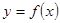 的顶点坐标为
的顶点坐标为 ,且
,且 的两个实根之差等于
的两个实根之差等于 ,
, __________.
__________.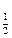 (a2-ax+2a)在[1,+∞
(a2-ax+2a)在[1,+∞ 上为减函数,则实数a的取值范围是( )
上为减函数,则实数a的取值范围是( )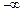 ,0)
,0)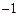 ,0)
,0)
 则不等式
则不等式 的解集为
的解集为  ,
, ,则
,则 等于( )
等于( ) ;
; ;
; ;
; .
.