题目内容
【题目】在平面直角坐标系xOy中,双曲线![]() (a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
(a,b>0)的左右焦点分别为F1(-c,0),F2(c,0),左顶点为A,左准线为l,过F1作直线交双曲线C左支于P,Q两点,则下列命题正确的是( )
A.若PQ⊥x轴,则△PQF2的周长为![]()
B.连PA交l于D,则必有QD//x轴
C.若PQ中点为M,则必有PQ⊥MF2
D.连PO交双曲线C右支于点N,则必有PQ//NF2
【答案】AD
【解析】
结合图象分析当PQ⊥x轴时,求出△PQF2的周长,通过证明四边形![]() 为平行四边形,得PQ//NF2,结合双曲线图像性质判定BC.
为平行四边形,得PQ//NF2,结合双曲线图像性质判定BC.
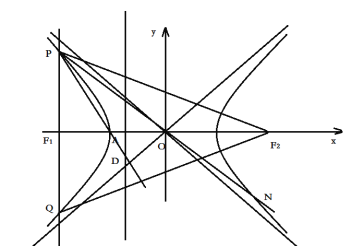
根据上图,若PQ⊥x轴,![]() ,则△PQF2的周长为
,则△PQF2的周长为![]() ,所以A选项正确;
,所以A选项正确;
连PA交l于D,则必有QD//x轴,由上图可得选项![]() 说法错误;
说法错误;
若PQ中点为M,则必有PQ⊥MF2,
假设该命题成立,则MF2是线段的PQ的垂直平分线,所以![]() ,根据双曲线的对称性可知,当且仅当PQ⊥x轴时成立,所以选项
,根据双曲线的对称性可知,当且仅当PQ⊥x轴时成立,所以选项![]() 错误;
错误;
连PO交双曲线C右支于点N,则必有PQ//NF2,考虑四边形PF1NF2,![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以有PQ//NF2.故选项
,所以有PQ//NF2.故选项![]() 正确.
正确.
故选:AD

 名校课堂系列答案
名校课堂系列答案【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得数据如下表(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(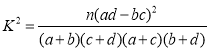 ,其中
,其中 ![]() )
)
抗倒伏数据如下:
143 147 147 151 153 153 157 159 160 164 166 169 174 175 175
180 188 188 192 195 195 199 203 206 206
易倒伏数据如下:
151 167 175 178 181 182 186 186 187 190 190 193 194 195 198
199 199 202 202 203
(1)完成 2×2 列联表,并说明能否在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,再从这9株中取出两株进行杂交试验,设取出的易倒伏玉米株数为X,求X的分布列(概率用组合数算式表示);
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差.