题目内容
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(Ⅰ )![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ )取AD中点为O,连接CO,PO,由已知可得CO⊥AD,PO⊥AD.以O为坐标原点,建立空间直角坐标系,求得P(0,0,1),B(1,1,0),D(0,﹣1,0),C(2,0,0),进一步求出向量![]() 的坐标,再求出平面PCD的法向量
的坐标,再求出平面PCD的法向量![]() ,设PB与平面PCD的夹角为θ,由
,设PB与平面PCD的夹角为θ,由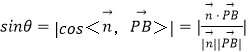 求得直线PB与平面PCD所成角的正弦值;
求得直线PB与平面PCD所成角的正弦值;
(Ⅱ)假设存在M点使得BM∥平面PCD,设![]() ,M(0,y1,z1),由
,M(0,y1,z1),由![]() 可得M(0,1﹣λ,λ),
可得M(0,1﹣λ,λ),![]() ,由BM∥平面PCD,可得
,由BM∥平面PCD,可得
![]() ,由此列式求得当
,由此列式求得当![]() 时,M点即为所求.
时,M点即为所求.
详解:(1)取AD的中点O,连接PO,CO.
因为PA=PD,所以PO⊥AD.
又因为PO平面PAD,平面PAD⊥平面ABCD,
所以PO⊥平面ABCD.
因为CO平面ABCD,所以PO⊥CO.
因为AC=CD,所以CO⊥AD.
以O为坐标原点,建立空间直角坐标系如图:
则P(0,0,1),B(1,1,0),D(0,﹣1,0),C(2,0,0),
则![]() ,
,![]() ,
,
设![]() 为平面PCD的法向量,
为平面PCD的法向量,
则由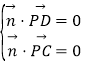 ,得
,得![]() ,则
,则![]() .
.
设PB与平面PCD的夹角为θ,则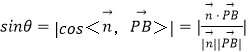 =
=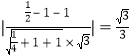 ;
;
(2) 假设存在M点使得BM∥平面PCD,设![]() ,M(0,y1,z1),
,M(0,y1,z1),
由(Ⅱ)知,A(0,1,0),P(0,0,1),![]() ,B(1,1,0),
,B(1,1,0),![]() ,
,
则有![]() ,可得M(0,1﹣λ,λ),
,可得M(0,1﹣λ,λ),
∴![]() ,
,
∵BM∥平面PCD,![]() 为平面PCD的法向量,
为平面PCD的法向量,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
综上,存在点M,即当![]() 时,M点即为所求.
时,M点即为所求.

【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间![]() 与每天获得的利润
与每天获得的利润![]() (单位:万元)的有关数据.
(单位:万元)的有关数据.
星期 | 星期2 | 星期3 | 星期4 | 星期5 | 星期6 |
利润 | 2 | 3 | 5 | 6 | 9 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(2)估计星期日获得的利润为多少万元.
参考公式: 
