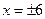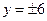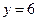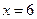题目内容
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件: |F2A|、|F2B|、|F2C|成等差数列.
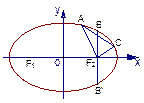
(1)求该弦椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.

(1)求该弦椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
(1)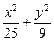 ="1" (2)
="1" (2)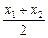 ="4" (3) -
="4" (3) -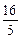 <m<
<m<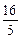
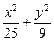 ="1" (2)
="1" (2)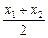 ="4" (3) -
="4" (3) -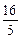 <m<
<m<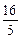
(1)由椭圆定义及条件知,2a=|F1B|+|F2B|=10,得a=5,又c=4,所以b=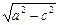 =3.
=3.
故椭圆方程为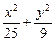 =1.
=1.
(2)由点B(4,yB)在椭圆上,得|F2B|=|yB|=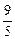 . 因为椭圆右准线方程为x=
. 因为椭圆右准线方程为x=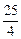 ,离心率为
,离心率为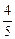 ,根据椭圆定义,有|F2A|=
,根据椭圆定义,有|F2A|=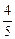 (
(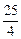 -x1),|F2C|=
-x1),|F2C|=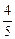 (
(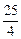 -x2),
-x2),
由|F2A|、|F2B|、|F2C|成等差数列,得
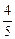 (
(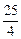 -x1)+
-x1)+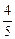 (
(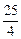 -x2)=2×
-x2)=2×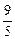 ,由此得出: x1+x2=8.
,由此得出: x1+x2=8.
设弦AC的中点为P(x0,y0),则x0=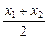 =4.
=4.
(3)解法一: 由A(x1,y1),C(x2,y2)在椭圆上.
得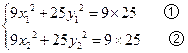
①-②得9(x12-x22)+25(y12-y22)=0,
即9×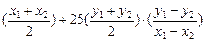 =0(x1≠x2)
=0(x1≠x2)
将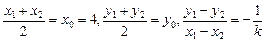 (k≠0)
(k≠0)
代入上式,得9×4+25y0(-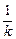 )="0 " (k≠0)
)="0 " (k≠0)
即k=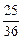 y0(当k=0时也成立).
y0(当k=0时也成立).
由点P(4,y0)在弦AC的垂直平分线上,得y0=4k+m,
所以m=y0-4k=y0-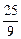 y0=-
y0=-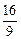 y0.
y0.
由点P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,
得-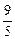 <y0<
<y0<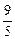 ,所以-
,所以-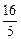 <m<
<m<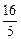 .
.
解法二: 因为弦AC的中点为P(4,y0),所以直线AC的方程为
y-y0=-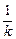 (x-4)(k≠0) ③
(x-4)(k≠0) ③
将③代入椭圆方程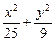 =1,得
=1,得
(9k2+25)x2-50(ky0+4)x+25(ky0+4)2-25×9k2=0
所以x1+x2=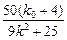 =8,解得k=
=8,解得k=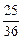 y0. (当k=0时也成立)
y0. (当k=0时也成立)
(以下同解法一).
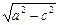 =3.
=3.故椭圆方程为
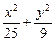 =1.
=1.(2)由点B(4,yB)在椭圆上,得|F2B|=|yB|=
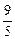 . 因为椭圆右准线方程为x=
. 因为椭圆右准线方程为x=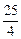 ,离心率为
,离心率为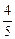 ,根据椭圆定义,有|F2A|=
,根据椭圆定义,有|F2A|=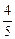 (
(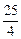 -x1),|F2C|=
-x1),|F2C|=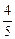 (
(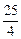 -x2),
-x2),由|F2A|、|F2B|、|F2C|成等差数列,得
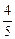 (
(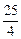 -x1)+
-x1)+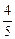 (
(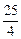 -x2)=2×
-x2)=2×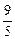 ,由此得出: x1+x2=8.
,由此得出: x1+x2=8.设弦AC的中点为P(x0,y0),则x0=
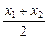 =4.
=4.(3)解法一: 由A(x1,y1),C(x2,y2)在椭圆上.
得
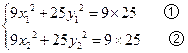
①-②得9(x12-x22)+25(y12-y22)=0,
即9×
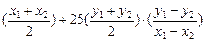 =0(x1≠x2)
=0(x1≠x2)将
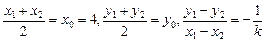 (k≠0)
(k≠0)代入上式,得9×4+25y0(-
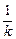 )="0 " (k≠0)
)="0 " (k≠0)即k=
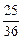 y0(当k=0时也成立).
y0(当k=0时也成立).由点P(4,y0)在弦AC的垂直平分线上,得y0=4k+m,
所以m=y0-4k=y0-
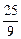 y0=-
y0=-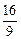 y0.
y0.由点P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,
得-
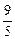 <y0<
<y0<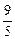 ,所以-
,所以-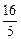 <m<
<m<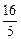 .
.解法二: 因为弦AC的中点为P(4,y0),所以直线AC的方程为
y-y0=-
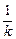 (x-4)(k≠0) ③
(x-4)(k≠0) ③将③代入椭圆方程
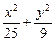 =1,得
=1,得(9k2+25)x2-50(ky0+4)x+25(ky0+4)2-25×9k2=0
所以x1+x2=
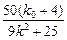 =8,解得k=
=8,解得k=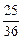 y0. (当k=0时也成立)
y0. (当k=0时也成立)(以下同解法一).

练习册系列答案
相关题目
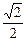 ,1)
,1)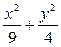 =1上一点,F1、F2是椭圆的两个焦点,则cosF1PF2的最小值是( )
=1上一点,F1、F2是椭圆的两个焦点,则cosF1PF2的最小值是( )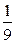
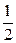
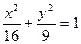 ,点A、B是它的两个焦点,当静止的小球放在点A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的最短路程是( ).
,点A、B是它的两个焦点,当静止的小球放在点A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的最短路程是( ).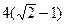
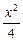 +y2=1相交于A、B两点,则|AB|的最大值为( )
+y2=1相交于A、B两点,则|AB|的最大值为( )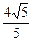


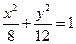 的准线方程是( )
的准线方程是( )