题目内容
(本小题满分14分)设圆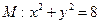 ,将曲线上每一点的纵坐标压缩到原来的
,将曲线上每一点的纵坐标压缩到原来的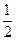 ,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线
,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线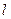 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交曲线C于A、B两个不同点.
交曲线C于A、B两个不同点.
(1)求曲线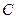 的方程;
的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
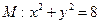 ,将曲线上每一点的纵坐标压缩到原来的
,将曲线上每一点的纵坐标压缩到原来的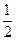 ,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线
,对应的横坐标不变,得到曲线C.经过点M(2,1),平行于OM的直线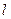 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交曲线C于A、B两个不同点.
交曲线C于A、B两个不同点.(1)求曲线
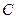 的方程;
的方程;(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
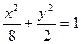

解:(1)在曲线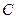 上任取一个动点P(x,y),则点(x,2y)在圆
上任取一个动点P(x,y),则点(x,2y)在圆 上.所以有
上.所以有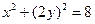 .整理得曲线C的方程为
.整理得曲线C的方程为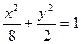 .
.
它表示一个焦点在x轴上的椭圆. …………4分
(2)∵直线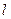 平行于OM,且在y轴上的截距为m,又
平行于OM,且在y轴上的截距为m,又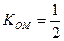 ,
,
∴直线 的方程为
的方程为 . …………6分
. …………6分
由 , …………7分
, …………7分
∵直线 与椭圆交于A、B两个不同点,
与椭圆交于A、B两个不同点, …………8分
…………8分
解得 .∴m的取值范围是
.∴m的取值范围是 . …………10分
. …………10分
(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.
设

 ,
, 可得
可得 .……12分
.……12分

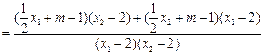

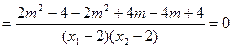 .
.
k1+k2=0.故直线MA、MB与x轴始终围成一个等腰三角形. …………14分
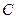 上任取一个动点P(x,y),则点(x,2y)在圆
上任取一个动点P(x,y),则点(x,2y)在圆 上.所以有
上.所以有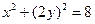 .整理得曲线C的方程为
.整理得曲线C的方程为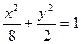 .
.它表示一个焦点在x轴上的椭圆. …………4分
(2)∵直线
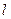 平行于OM,且在y轴上的截距为m,又
平行于OM,且在y轴上的截距为m,又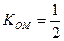 ,
,∴直线
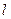 的方程为
的方程为 . …………6分
. …………6分由
 , …………7分
, …………7分∵直线
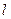 与椭圆交于A、B两个不同点,
与椭圆交于A、B两个不同点, …………8分
…………8分解得
 .∴m的取值范围是
.∴m的取值范围是 . …………10分
. …………10分(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.
设


 ,
, 可得
可得 .……12分
.……12分
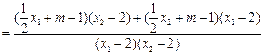

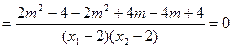 .
.k1+k2=0.故直线MA、MB与x轴始终围成一个等腰三角形. …………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
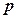 :“方程
:“方程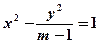 表示焦点在
表示焦点在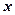 轴上的双曲线”,命题
轴上的双曲线”,命题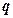 :“在区间
:“在区间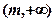 上,函数
上,函数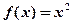 单调递增”,若
单调递增”,若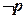 是真命题,
是真命题,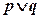 是真命题,求实数
是真命题,求实数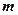 的取值范围。
的取值范围。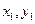 ),B(
),B(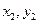 )是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为
)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为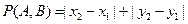 .
.
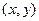 满足:
满足: ,求点P的轨迹方程。
,求点P的轨迹方程。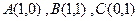 ,映射
,映射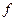 将
将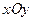 平面上的点
平面上的点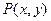 对应到另一个平面直角坐标系
对应到另一个平面直角坐标系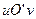 上的点
上的点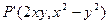 ,则当点
,则当点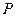 沿着折线
沿着折线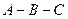 运动时,在映射
运动时,在映射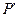 的轨迹是
的轨迹是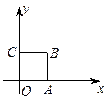
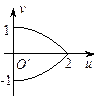
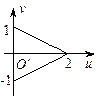
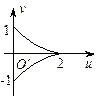
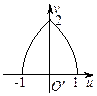
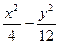 =1的焦点为顶点,顶点为焦点的椭圆方程为 ( )
=1的焦点为顶点,顶点为焦点的椭圆方程为 ( )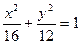 B.
B. 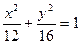 C.
C. 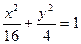 D.
D.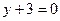 相切的动圆圆心轨迹方程是( )
相切的动圆圆心轨迹方程是( )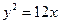
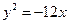
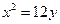
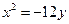
 是圆
是圆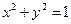 上的一个动点,过点
上的一个动点,过点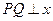 轴于点
轴于点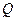 ,设
,设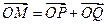 ,则点
,则点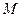 的轨迹方程______________;
的轨迹方程______________;