题目内容
定义在R上的函数f（x）满足f（1）=2，且在定义域上恒有f′（x）＜2成立，则不等式f（2x）＜4x的解集为（ ）
| A．（-∞，1） | B．（1，+∞） | C．（-∞，
| D．（
|
设F（x）=f（x）-2x，则：F'（x）=f'（x）-2＜0
即：F（x）R上的是减函数，且F（1）=f（1）-2×1=0
∴当x＜1时，F（x）=f（x）-2x＞F（1）=0，即：f（x）＞2x；
当x＞1时，F（x）=f（x）-2x＜F（1）=0，即：f（x）＜2x；
∴不等式f（2x）＜4x的解集为：2x＞1，即x＞
；
故选：D．
即：F（x）R上的是减函数，且F（1）=f（1）-2×1=0
∴当x＜1时，F（x）=f（x）-2x＞F（1）=0，即：f（x）＞2x；
当x＞1时，F（x）=f（x）-2x＜F（1）=0，即：f（x）＜2x；
∴不等式f（2x）＜4x的解集为：2x＞1，即x＞
| 1 |
| 2 |
故选：D．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
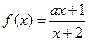在区间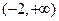
上是增函数，则
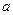的取值范围是 。
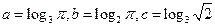，则 
