题目内容
5. 圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.
圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.
分析 设出球的半径,三个球的体积和水的体积之和,等于柱体的体积,求解即可.
解答 解:设球半径为r,则由3V球+V水=V柱可得3×$\frac{4}{3}π{r}^{3}+π{r}^{2}×8=π{r}^{2}×6r$,解得r=4.
故答案为:4.
点评 本题考查几何体的体积,考查学生空间想象能力,是基础题.

练习册系列答案
相关题目
16.如表是某厂1-4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有线性相关关系,其线性回归方程是$\widehat{y}$=-0.7x+$\widehat{a}$,则$\widehat{a}$=( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 5.15 | B. | 5.20 | C. | 5.25 | D. | 5.30 |
10.下列集合中,结果是空集的是( )
| A. | {x∈R|x2-1=0} | B. | {x|x>6或x<1} | C. | {(x,y)|x2+y2=0} | D. | {x|x>6且x<1} |
14.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
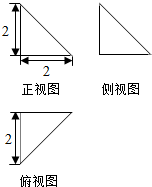

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
15.设点P是Z轴上一点,且点P到M(1,0,2)与点N(1,-3,1)的距离相等,则点P的坐标是( )
| A. | (-3,-3,0) | B. | (0,0,3) | C. | (0,-3,-3) | D. | (0,0,-3) |
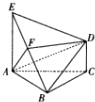 如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.
如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.