题目内容
已知直线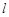 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)若 是直线
是直线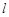 与圆面
与圆面 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围.
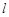 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.(1)求圆
 的直角坐标方程;
的直角坐标方程;(2)若
 是直线
是直线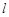 与圆面
与圆面 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围.(1)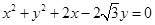 ;(2)
;(2)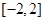
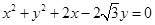 ;(2)
;(2)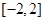
试题分析: (1)根据公式
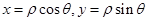 将极坐标方程转化为直角坐标方程。(2)法一:设
将极坐标方程转化为直角坐标方程。(2)法一:设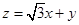 ,将圆
,将圆 的一般方程化为标准方程即可得圆心
的一般方程化为标准方程即可得圆心 的坐标和圆的半径。将直线
的坐标和圆的半径。将直线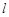 化为普通方程。联立方程组可得两交点坐标。根据题意可知点
化为普通方程。联立方程组可得两交点坐标。根据题意可知点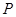 即在这两点连线的线段上。将两交点坐标代入
即在这两点连线的线段上。将两交点坐标代入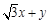 即可得其最值。
即可得其最值。试题解析:(1)因为圆
 的极坐标方程为
的极坐标方程为
所以
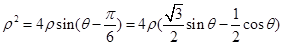
又
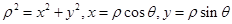
所以
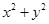
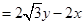
所以圆
 的普通方程
的普通方程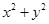
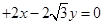
(2)『解法1』:
设
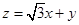
由圆
 的方程
的方程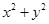
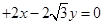
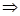
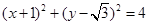
所以圆
 的圆心是
的圆心是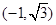 ,半径是
,半径是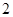
将
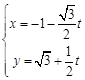 代入
代入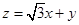 得
得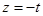
又直线
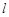 过
过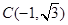 ,圆
,圆 的半径是
的半径是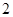 ,所以
,所以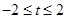
所以
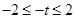
即
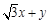 的取值范围是
的取值范围是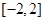
『解法2』:
直线
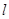 的参数方程化成普通方程为:
的参数方程化成普通方程为: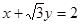 6分
6分由
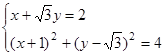 ,
,解得
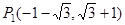 ,
,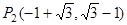 8分
8分∵
 是直线
是直线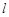 与圆面
与圆面 的公共点,
的公共点,∴点
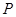 在线段
在线段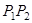 上,
上,∴
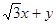 的最大值是
的最大值是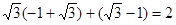 ,
,最小值是
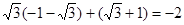
∴
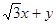 的取值范围是
的取值范围是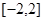 10分
10分
练习册系列答案
相关题目
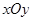 ,以
,以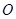 为极点,
为极点,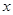 轴的非负半轴为极轴建立极坐标系,,曲线
轴的非负半轴为极轴建立极坐标系,,曲线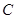 的参数方程为
的参数方程为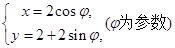 .点
.点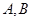 是曲线
是曲线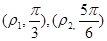 .
.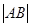 的值.
的值.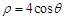 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: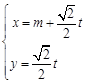 (
(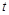 是参数).
是参数).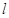 的参数方程化为普通方程;
的参数方程化为普通方程;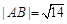 ,试求实数m值.
,试求实数m值.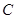 的极坐标方程是
的极坐标方程是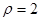 ,以极点为原点,极轴为
,以极点为原点,极轴为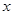 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线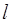 的参数方程为
的参数方程为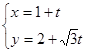 (
(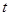 为参数).
为参数).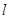 的普通方程与曲线
的普通方程与曲线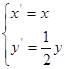 得到曲线
得到曲线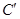 ,设
,设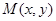 为曲线
为曲线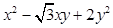 的最小值,并求相应点
的最小值,并求相应点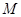 的坐标.
的坐标.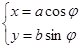 (a>b>0,
(a>b>0,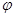 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M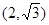 对应的参数
对应的参数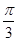 ,
,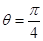 与曲线C2交于点D
与曲线C2交于点D
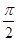 )是曲线C1上的两点,求
)是曲线C1上的两点,求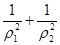 的值。
的值。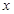 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线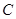 的参数方程为
的参数方程为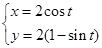 (其中
(其中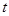 为参数,且
为参数,且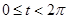 ),则曲线
),则曲线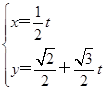 (t为参数),若以直角坐标系的原点O为极点,x轴非负半轴为极轴,且长度单位相同,建立极坐标系,曲线C的极坐标方程为ρ=2cos
(t为参数),若以直角坐标系的原点O为极点,x轴非负半轴为极轴,且长度单位相同,建立极坐标系,曲线C的极坐标方程为ρ=2cos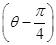 .若直线l与曲线C交于A,B两点,则|AB|=________.
.若直线l与曲线C交于A,B两点,则|AB|=________.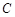 的极坐标方程为
的极坐标方程为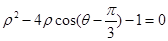 ,若以极点为原点,以极轴为
,若以极点为原点,以极轴为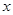 轴的正半轴建立相应的平面直角坐标系
轴的正半轴建立相应的平面直角坐标系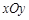 ,则在直角坐标系中,圆心
,则在直角坐标系中,圆心