题目内容
在平面直角坐标系中，直线l的参数方程为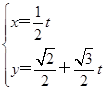
(t为参数)，若以直角坐标系的原点O为极点，x轴非负半轴为极轴，且长度单位相同，建立极坐标系，曲线C的极坐标方程为ρ＝2cos
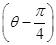.若直线l与曲线C交于A，B两点，则|AB|＝________.
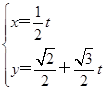(t为参数)，若以直角坐标系的原点O为极点，x轴非负半轴为极轴，且长度单位相同，建立极坐标系，曲线C的极坐标方程为ρ＝2cos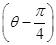.若直线l与曲线C交于A，B两点，则|AB|＝________.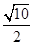
首先消去参数t，可得直线方程为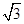
x－y＋
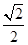＝0，极坐标方程化为直角坐标方程为
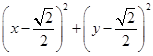＝1，根据直线与圆的相交弦长公式可得
|AB|＝2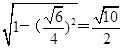
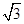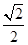x－y＋＝0，极坐标方程化为直角坐标方程为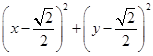＝1，根据直线与圆的相交弦长公式可得|AB|＝2
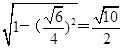
练习册系列答案
名校课堂系列答案
相关题目
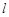的参数方程为
为参数)，以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，圆
的极坐标方程为
．
的直角坐标方程；
是直线
≤
的公共点，求
的取值范围．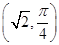
，直线的极坐标方程为ρcos
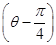＝a，且点A在直线上．
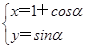，(α为参数)，试判断直线与圆的位置关系．
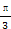)=6,圆C的参数方程为
(θ为参数),求直线l被圆C截得的弦长.
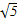,求a的值.
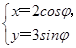(φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2.正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为
，
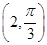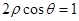与圆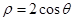
相交的弦长为 
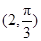和圆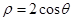
的圆心的距离为( )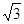
（
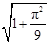
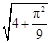
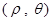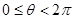）中，直线
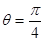被圆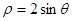
截得的弦长是 ．