题目内容
已知曲线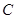 的极坐标方程是
的极坐标方程是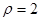 ,以极点为原点,极轴为
,以极点为原点,极轴为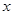 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线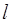 的参数方程为
的参数方程为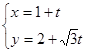 (
(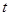 为参数).
为参数).
(Ⅰ)写出直线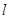 的普通方程与曲线
的普通方程与曲线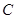 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线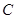 经过伸缩变换
经过伸缩变换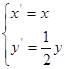 得到曲线
得到曲线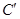 ,设
,设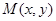 为曲线
为曲线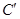 上任一点,求
上任一点,求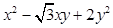 的最小值,并求相应点
的最小值,并求相应点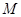 的坐标.
的坐标.
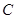 的极坐标方程是
的极坐标方程是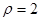 ,以极点为原点,极轴为
,以极点为原点,极轴为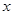 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线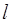 的参数方程为
的参数方程为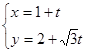 (
(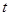 为参数).
为参数).(Ⅰ)写出直线
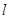 的普通方程与曲线
的普通方程与曲线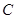 的直角坐标方程;
的直角坐标方程;(Ⅱ)设曲线
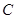 经过伸缩变换
经过伸缩变换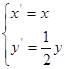 得到曲线
得到曲线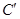 ,设
,设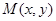 为曲线
为曲线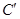 上任一点,求
上任一点,求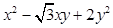 的最小值,并求相应点
的最小值,并求相应点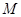 的坐标.
的坐标.(1)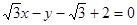 ,
, 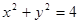 ;(2)当
;(2)当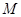 为(
为(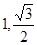 )或
)或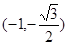 ,
,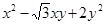 的最小值为1.
的最小值为1.
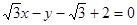 ,
, 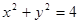 ;(2)当
;(2)当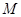 为(
为(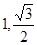 )或
)或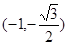 ,
,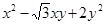 的最小值为1.
的最小值为1.试题分析:(1)把直线
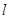 的参数方程化为普通方程,关键消去参数,由一个方程表示出
的参数方程化为普通方程,关键消去参数,由一个方程表示出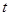 ,再代入另一个方程,即的普通方程,将极坐标方程化为直角坐标方程,关键熟练掌握
,再代入另一个方程,即的普通方程,将极坐标方程化为直角坐标方程,关键熟练掌握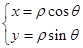 ,故将
,故将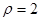 两边同时平方,即化为直角坐标方程;(2)先求曲线
两边同时平方,即化为直角坐标方程;(2)先求曲线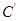 的方程
的方程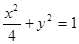 ,然后利用椭圆的参数方程,设为
,然后利用椭圆的参数方程,设为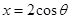
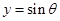 ,代入所求式中,转化为三角函数的最值问题处理.
,代入所求式中,转化为三角函数的最值问题处理.试题解析:(1)由
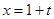 ,得
,得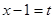 ,代入
,代入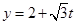 ,得直线的普通方程
,得直线的普通方程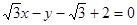 , 由
, 由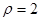 两边同时平方,得
两边同时平方,得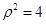 ,将
,将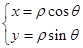 代入,得
代入,得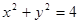 .
.(2)
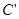 :
: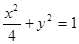 , 设
, 设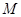 为:
为: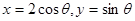 ,则
,则 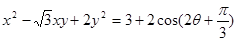
所以当
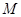 为(
为(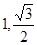 )或
)或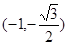 ,
,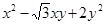 的最小值为1.
的最小值为1.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
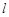 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
. 的直角坐标方程;
的直角坐标方程; 是直线
是直线 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围.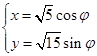 (
(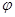 为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点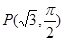 ,直线
,直线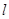 的极坐标方程为
的极坐标方程为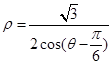 .
.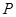 与直线
与直线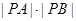 的值.
的值.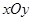 中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为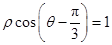 ,M,N分别为C与x轴,y轴的交点.
,M,N分别为C与x轴,y轴的交点.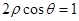 与圆
与圆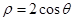 相交的弦长为
相交的弦长为 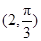 和圆
和圆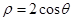 的圆心的距离为( )
的圆心的距离为( )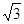
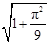
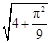
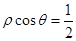 与曲线
与曲线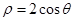 相交于
相交于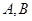 两点,
两点,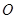 为极点,则
为极点,则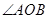 的大小为 .
的大小为 .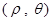 (
(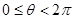 )中,直线
)中,直线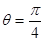 被圆
被圆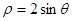 截得的弦长是 .
截得的弦长是 .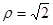 截直线
截直线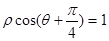 所得的弦长为 .
所得的弦长为 .