题目内容
“m=0”是“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”的______条件.
当m=0时,两直线的方程分别为y-5=0,与2x-1=0,可得出此两直线是垂直的
当两直线垂直时,当m=0时,符合题意,当m≠0时且m≠1时,两直线的斜率分别是
与-
,由两直线垂直得
×
=1得m=-
由上证,“m=0”可得出“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”,由“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”可得出“m=0或m=-
”,
所以“m=0”是“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”的必要非充分条件
故答案为:必要非充分
当两直线垂直时,当m=0时,符合题意,当m≠0时且m≠1时,两直线的斜率分别是
| m |
| 1-m |
| m+2 |
| m |
| m |
| 1-m |
| m+2 |
| m |
| 1 |
| 2 |
由上证,“m=0”可得出“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”,由“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”可得出“m=0或m=-
| 1 |
| 2 |
所以“m=0”是“直线mx+(m-1)y+5=0与直线(m+2)x+my-1=0互相垂直”的必要非充分条件
故答案为:必要非充分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
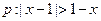 ,条件
,条件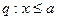 ,若p是非q的充分不必要条件,则a的取值范围是
,若p是非q的充分不必要条件,则a的取值范围是