题目内容
己知命题p:x2-8x-20≤0;命题q:[x-(1-m)][x-(1+m)]≤0(m>0).若?p是?q的必要不充分条件,求实数m的取值范围.
由p:x2-8x-20≤0;得(x+2)(x-10)≤0,即-2≤x≤10.
由q:[x-(1-m)][x-(1+m)]≤0(m>0).得1-m≤x≤1+m,m>0.
∵?p是?q的必要不充分条件,
∴q是p的必要不充分条件,
即
,
解得
,即m≥9,
∴实数m的取值范围是m≥9.
由q:[x-(1-m)][x-(1+m)]≤0(m>0).得1-m≤x≤1+m,m>0.
∵?p是?q的必要不充分条件,
∴q是p的必要不充分条件,
即
|
解得
|
∴实数m的取值范围是m≥9.

练习册系列答案
相关题目
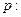 不等式
不等式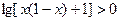 的解集为
的解集为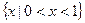 ;命题
;命题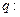 在
在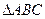 中,
中,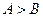 是
是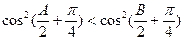 成立的必要不充分条件.则
成立的必要不充分条件.则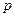 真
真 假
假