题目内容
已知a＜b函数f（x）=sinx，g（x）=cosx，若命题p：f（a）f（b）＜0，命题q：g（x）在（a，b）内有最值，则命题p是命题q成立的（ ）条件．
| A．充分不必要 | B．必要不充分 |
| C．充要 | D．既不充分也不必要 |
∵f（a）•f（b）＜0，∴根据函数的零点判定定理可知，函数f（x）在（a，b）上存在零点，
根据正弦函数、余弦函数的性质可知，正弦函数的零点是余弦函数的最值点，
∴g（x）=cosx在（a，b）上有最值，所以成立．
若g（x）=cosx在（a，b）上有最值，则根据余弦函数的最值点是正弦函数的零点．
则f（x）=sinx在（a，b）上有零点，但是由于函数f（x）=sinx在（a，b）不一定单调，f（a）f（b）＜0不一定成立．
所以命题p是命题q成立的充分不必要条件．
故选A．
根据正弦函数、余弦函数的性质可知，正弦函数的零点是余弦函数的最值点，
∴g（x）=cosx在（a，b）上有最值，所以成立．
若g（x）=cosx在（a，b）上有最值，则根据余弦函数的最值点是正弦函数的零点．
则f（x）=sinx在（a，b）上有零点，但是由于函数f（x）=sinx在（a，b）不一定单调，f（a）f（b）＜0不一定成立．
所以命题p是命题q成立的充分不必要条件．
故选A．
练习册系列答案
相关题目
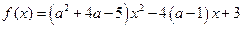的图象全在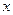
轴的上方成立的充要条件。