题目内容
以下给出的是用条件语句编写的程序,根据该程序回答
READx
IFx<aTHENy=-x2+ax+b
ELSEy=x2-ax+b
ENDIF
PRINTy
END
(Ⅰ)求证:输入x的值互为相反数则输出的y值也互为相反数的充要条件是a2+b2=0;
(Ⅱ)设常数b<2
-3,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.
READx
IFx<aTHENy=-x2+ax+b
ELSEy=x2-ax+b
ENDIF
PRINTy
END
(Ⅰ)求证:输入x的值互为相反数则输出的y值也互为相反数的充要条件是a2+b2=0;
(Ⅱ)设常数b<2
| 2 |
(I)充分性:若a2+b2=0时,即a=b=0,所以f(x)=x|x|.∵f(-x)=-x|-x|=-x|x|=-f(x),对一切x∈R恒成立,∴f(x)是奇函数;
必要性:若f(x)是奇函数,则对一切x∈R,f(-x)=-f(x)恒成立,即-x|-x-a|+b=-x|x-a|-b.
令x=0,得b=-b,所以b=0.
再令x=a,得2a|a|=0,∴a=0,即a2+b2=0.
(II)∵b<2
-3<0,∴当x=0时,a取任意实数不等式恒成立,
故考虑x∈(0,1]时,原不等式变为|x-a|<-
,即x+
<a<x-
.∴只需对x∈(0,1],满足
对(1)式,由b<0时,在(0,1]上,f(x)=x+
为增函数,∴(x+
)max=f(1)=1+b.∴a>1+b.(3)
对(2)式,当-1≤b<0时,在(0,1]上,x-
=x+
≥2
.
当x=
时,x-
=2
,∴(x-
)min=2
.∴a<2
.(4)
由(3)、(4),要使a存在,必须有
即-1≤b<-3+2
.
∴当-1≤b<-3+2
时,1+b<a<2
.
当b<-1时,在(0,1]上,f(x)=x-
为减函数,(证明略)
综上所述,当-1≤b<2
-3时,a的取值范围是(1+b,2
);
当b<-1时,a的取值范围是(1+b,1-b).
必要性:若f(x)是奇函数,则对一切x∈R,f(-x)=-f(x)恒成立,即-x|-x-a|+b=-x|x-a|-b.
令x=0,得b=-b,所以b=0.
再令x=a,得2a|a|=0,∴a=0,即a2+b2=0.
(II)∵b<2
| 2 |
故考虑x∈(0,1]时,原不等式变为|x-a|<-
| b |
| x |
| b |
| x |
| b |
| x |
|
对(1)式,由b<0时,在(0,1]上,f(x)=x+
| b |
| x |
| b |
| x |
对(2)式,当-1≤b<0时,在(0,1]上,x-
| b |
| x |
| -b |
| x |
| -b |
当x=
| -b |
| b |
| x |
| -b |
| b |
| x |
| 6 |
| -b |
由(3)、(4),要使a存在,必须有
|
| 2 |
∴当-1≤b<-3+2
| 2 |
| -b |
当b<-1时,在(0,1]上,f(x)=x-
| b |
| x |
|
综上所述,当-1≤b<2
| 2 |
| -b |
当b<-1时,a的取值范围是(1+b,1-b).

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 为实数,且
为实数,且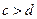 。则“
。则“ ”是“
”是“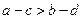 ”的( )
”的( )