题目内容
15．如图△ABC中，D是AB的一个三等分点，DE∥BC，EF∥DC，AF=2，则AB=$\frac{9}{2}$
分析 由D是AB的一个三等分点，DE∥BC，EF∥DC，可得$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{AF}{FD}$=2，结合AF=2，可得答案．
解答 解：∵D是AB的一个三等分点，DE∥BC，
$\frac{AD}{DB}$=$\frac{AE}{EC}$=2，
又∵EF∥DC，
∴$\frac{AE}{EC}$=$\frac{AF}{FD}$=2，
又∵AF=2，
∴FD=1，
∴DB=$\frac{3}{2}$，
∴AB=$\frac{9}{2}$，
故答案为：$\frac{9}{2}$
点评 本题考查的知识点是平行线分线段成比例定理，难度不大，属于基础题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
5．已知f（x）=$\left\{\begin{array}{l}（2a-1）x+4a，x＜1\\-x+1，x≥1\end{array}$是定义在R上的减函数，则a的取值范围是（ ）
| A． | $[\frac{1}{6}，\frac{1}{2}）$ | B． | $[\frac{1}{3}，\frac{1}{2}]$ | C． | $（\frac{1}{6}，\frac{1}{2}]$ | D． | $[\frac{1}{3}，\frac{1}{2}]$ |
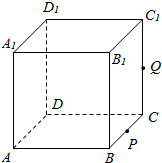如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则当CQ∈（0，$\frac{1}{2}$]∪{1}．时，S为四边形；当CQ=$\frac{1}{2}$时S为等腰梯形；当CQ=1时，S的面积为$\frac{\sqrt{6}}{2}$．
如图，设A是棱长为2的正方体的一个顶点，过从顶点A出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，截去8个三棱锥，所得的各截面与正方体各面共同围成一个多面体，则关于此多面体有以下结论：
20．设a=（lg3）2，b=30.3，c=lg$\sqrt{3}$，则（ ）
| A． | a＜c＜b | B． | c＜a＜b | C． | b＜a＜c | D． | b＜c＜a |
4．已知集合$A=\{x|x＞0\}，B=\{x|\frac{1}{2}＜{2^x}＜4\}$，则A∩∁RB=（ ）
| A． | {x|x＞0} | B． | {x|0＜x＜2} | C． | {x|x≥2} | D． | {x|x＞2} |