Question

10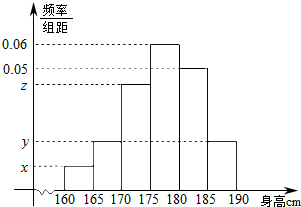．从某学校的800名男生中抽 取40名测量身高，并制成如下频率分布直方图，已知x：y：z=1：2：4．
（1）求调查对象中身高介于[165，175）之间的人数；
（2）估计该校男生中身高在180cm以上的人数；
（3）从抽取的身高在[160，170）之间的男生中任选3人，求至少有1人身高在[160，165）之间的概率．

Answer 1

分析 （1）根据频率分布直方图先求出x，即可求调查对象中身高介于[165，175）之间的人数；
（2）根据频率分布直方图进行即可即可；
（3）利用列举法结合古典概型的概率公式进行求解即可．

解答 解：（1）∵x：y：z=1：2：4，
∴（x+2x+4x+0.05+0.06+2x）×5=1，
解得x=0.01，
∴（y+z）×5×40=200×6x=12
即调查对象中身高介于[165，175）之间有12人．----------------------（3分）
（2）800×（0.05+0.02）×5=280人----------------------（6分）
（3）身高在[160，165）之间的人数为：40×0.01×5=2 人，设为A₁，A₂----（7分）
身高在[165，170）之间的人数为：40×0.02×5=4人，
设为B₁ B₂，B₃，B₄-------（8分）
从6人中任选3人共有：（A₁A₂B₁）（ A₁A₂B₂）（A₁A₂B₃）（A₁A₂B₄）
（A₁B₁B₂）（A₁B₁B₃）（A₁B₁B₄）（A₁B₂B₃）（A₁B₂B₄）（A₁B₃B₄）（A₂B₁B₂）
（A₂B₁B₃）（A₂B₁B₄）（A₂B₂B₃）（A₂B₂B₄）（A₂B₃B₄）（B₁B₂B₃）（B₁B₂B₄）
（B₁B₃B₄）（B₂B₃B₄）20种情况，----------------------（10分）
其中至少有1人身高在[160，165）之间有16种情况，----------------------（11分）
∴至少有1人身高在[160，165）之间的概率为$\frac{16}{20}=\frac{4}{5}$．----------------------（12分）

点评 本题主要考查频率分布直方图和概率的求解，利用列举法是解决本题的关键．