题目内容
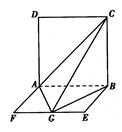
如图,ABCD是边长为2的正方形,ABEF是矩形,且二面角C—AB—F是直二面角,AF=1,G是EF的中点.
(1)求证:平面AGC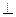 平面BGC;
平面BGC;
(2)求GB与平面AGC所成角的正弦值.

(1)求证:平面AGC
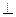 平面BGC;
平面BGC;(2)求GB与平面AGC所成角的正弦值.
1) 正方形ABCD,
正方形ABCD,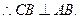
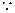 二面角C-AB-F是直二面角,
二面角C-AB-F是直二面角,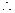 CB
CB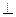 面ABEF.
面ABEF.
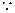 AG, GB
AG, GB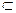 面ABEF,
面ABEF,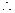 CB
CB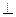 AG,CB
AG,CB BG,…………(2分)
BG,…………(2分)
又AD=2a,AF= a,ABEF是矩形,G是EF的中点,
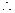
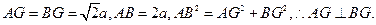 …………(4分)
…………(4分)
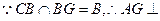 平面GBC,而
平面GBC,而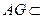 面ACG,
面ACG,
故平面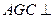 平面BGC. …………(6分)
平面BGC. …………(6分)
(2)由(1)知,面ACG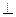 面BGC,且交于GC,在平面BGC内作BH
面BGC,且交于GC,在平面BGC内作BH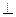 GC,垂足为H ,则BH
GC,垂足为H ,则BH 平面AGC.
平面AGC.
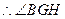 是BG与平面AGC所成的角, …………(8分)
是BG与平面AGC所成的角, …………(8分)
 在
在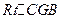 中,
中,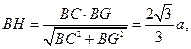
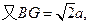 …………(10分)
…………(10分)
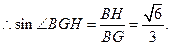 …………(12分)
…………(12分)
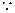 正方形ABCD,
正方形ABCD,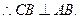
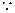 二面角C-AB-F是直二面角,
二面角C-AB-F是直二面角,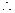 CB
CB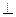 面ABEF.
面ABEF.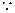 AG, GB
AG, GB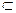 面ABEF,
面ABEF,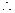 CB
CB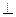 AG,CB
AG,CB BG,…………(2分)
BG,…………(2分)又AD=2a,AF= a,ABEF是矩形,G是EF的中点,
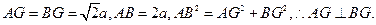 …………(4分)
…………(4分)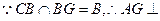 平面GBC,而
平面GBC,而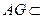 面ACG,
面ACG,故平面
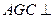 平面BGC. …………(6分)
平面BGC. …………(6分)(2)由(1)知,面ACG
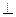 面BGC,且交于GC,在平面BGC内作BH
面BGC,且交于GC,在平面BGC内作BH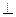 GC,垂足为H ,则BH
GC,垂足为H ,则BH 平面AGC.
平面AGC.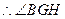 是BG与平面AGC所成的角, …………(8分)
是BG与平面AGC所成的角, …………(8分) 在
在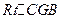 中,
中,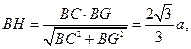
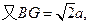 …………(10分)
…………(10分)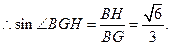 …………(12分)
…………(12分)略

练习册系列答案
相关题目
 的棱长为
的棱长为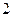 ,
,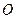 是
是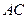 与
与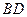 的交点,
的交点,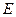 为
为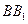 的中点.
的中点.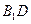 ∥平面
∥平面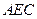 ;
;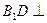 平面
平面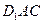 ;
;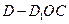 的体积.
的体积.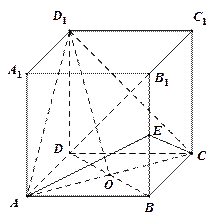
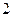 的正方体
的正方体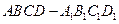 中,
中,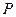 为棱
为棱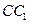 的中点,
的中点,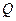 为正方形
为正方形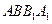 的中心,点
的中心,点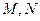 分别在直线
分别在直线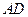 和
和 上.
上.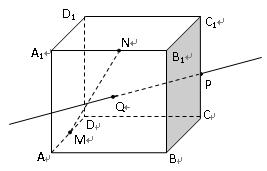
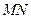 与
与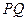 所成角的余弦值;
所成角的余弦值; 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
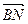 的长度;下
的长度;下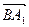 ,
, )的值;
)的值;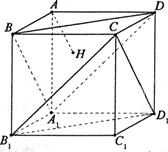
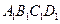 中心为
中心为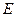 ,
,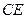 垂直,这样的直线可画
垂直,这样的直线可画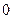 条
条 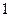 条
条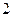 条
条 
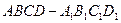 的12条棱中,与棱
的12条棱中,与棱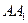 异面的棱共有
异面的棱共有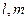 在平面
在平面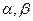 上射影分别为
上射影分别为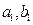 和
和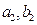 ,若
,若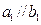 ,
,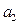 与
与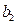 交于一点,则
交于一点,则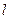 和
和 的位置关系为( )
的位置关系为( )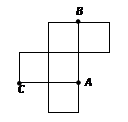 右图是一个无盖的正方体盒子展开后的平面图,
右图是一个无盖的正方体盒子展开后的平面图,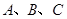 是展开图上的三点,则在正方形盒子中,
是展开图上的三点,则在正方形盒子中,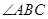 的值为( )
的值为( )