题目内容
如图是函数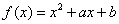 的部分图象,则函数
的部分图象,则函数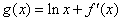 的零点所在的区间是( )
的零点所在的区间是( )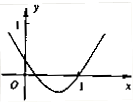
A. | B.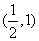 | C.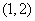 | D.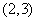 |
B
解析试题分析:由二次函数图象的对称轴确定a的范围,据g(x)的表达式计算g(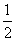 )和g(1)的值的符号,从而确定零点所在的区间.解:由函数f(x)=x2+ax+b的部分图象得0<b<1,f(1)=0,从而-2<a<-1,而g(x)=lnx+2x+a在定义域内单调递增, g(
)和g(1)的值的符号,从而确定零点所在的区间.解:由函数f(x)=x2+ax+b的部分图象得0<b<1,f(1)=0,从而-2<a<-1,而g(x)=lnx+2x+a在定义域内单调递增, g(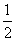 )=ln
)=ln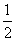 +1+a<0, g(1)=ln1+2+a=2+a>0,∴函数g(x)=lnx+f′(x)的零点所在的区间是
+1+a<0, g(1)=ln1+2+a=2+a>0,∴函数g(x)=lnx+f′(x)的零点所在的区间是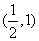 ;故选B.
;故选B.
考点:导数的运算
点评:本题主要考查了导数的运算,以及函数零点的判断,同时考查了运算求解能力和识图能力,属于基础题.

练习册系列答案
相关题目
方程2x-x2=0的解的个数是( )
| A.1 | B.2 |
| C.3 | D.4 |
函数f(x)=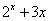 的零点所在的一个区间是
的零点所在的一个区间是
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
函数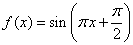 ,
,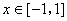 ,则
,则
A.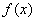 为偶函数,且在 为偶函数,且在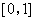 上单调递减 上单调递减 |
B.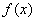 为偶函数,且在 为偶函数,且在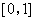 上单调递增 上单调递增 |
C.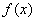 为奇函数,且在 为奇函数,且在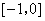 上单调递增 上单调递增 |
D.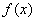 为奇函数,且在 为奇函数,且在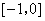 上单调递减 上单调递减 |
函数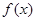 的图象如图所示,下列数值排序正确的是
的图象如图所示,下列数值排序正确的是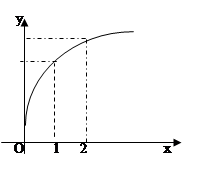
A.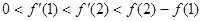 |
B.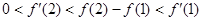 |
C.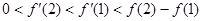 |
D.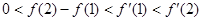 |
已知函数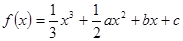 在
在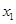 处取得极大值,在
处取得极大值,在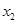 处取得极小值,满足
处取得极小值,满足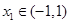 ,
,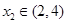 ,则
,则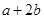 的取值范围是
的取值范围是
A.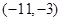 | B.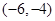 | C.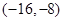 | D.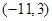 |
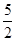 )=( )
)=( )
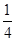
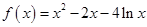 ,不等式
,不等式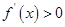 的解集为
的解集为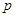 ,关于
,关于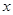 的不等式
的不等式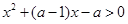 的解集记为
的解集记为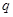 ,已知
,已知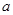 的取值范围是( )
的取值范围是( )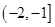
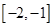
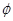
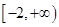
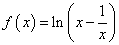 的图象是
的图象是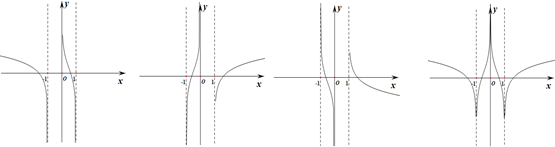 A. B. C. D.
A. B. C. D.