题目内容
方程2x-x2=0的解的个数是( )
| A.1 | B.2 |
| C.3 | D.4 |
C
解析试题分析:原方程可化为:2x=x2,在同一坐标系中画出函数y=2x与y=x2的图象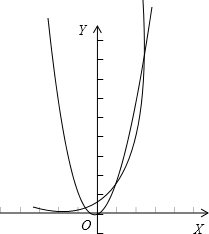
如图所示:由图象可得,两个函数的图象共有3个交点,一个点的横坐标小于0,另一个的横坐标为2,还有横坐标一个是4;故方程x2-2x=0的实数解的个数是3个,故选C.
考点:本题考查了函数根的个数及判定方法
点评:在判断复杂方程根的个数的时候,根据方程的根与函数零点个数的关系,可将问题转化为求函数零点个数问题,是常用方法,要熟练掌握.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
函数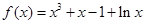 的零点所在的大致区间为
的零点所在的大致区间为
A.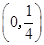 | B.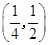 |
C.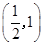 | D.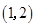 |
已知定义在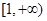 上的函数
上的函数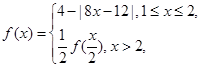 则
则
A.函数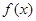 的值域为 的值域为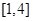 |
B.关于x的方程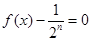 ( (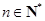 )有4个不相等的实数根 )有4个不相等的实数根 |
C.存在实数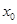 ,使得不等式 ,使得不等式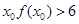 成立 成立 |
D.当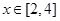 时,函数 时,函数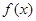 的图象与x轴围成的面积为1 的图象与x轴围成的面积为1 |
函数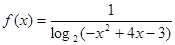 的定义域为( )
的定义域为( )
| A.(1,2)∪(2,3) | B.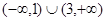 |
| C.(1,3) | D.[1,3] |
方程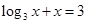 的解所在的区间是 ( )
的解所在的区间是 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,+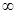 ) ) |
若函数 的导函数
的导函数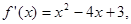 则函数
则函数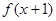 的单调递减区间是( )
的单调递减区间是( )
| A.(2,4) | B.(-3,-1) | C.(1,3) | D.(0,2) |
下列函数在其定义域内,既是奇函数又存在零点的是: ( )
A. | B.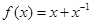 | C.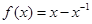 | D.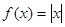 |
如图是函数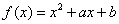 的部分图象,则函数
的部分图象,则函数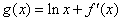 的零点所在的区间是( )
的零点所在的区间是( )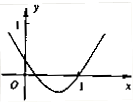
A. | B.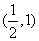 | C.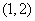 | D.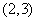 |
 在定义域内可导,
在定义域内可导,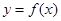 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数 的图象可能是( )
的图象可能是( )