题目内容
已知函数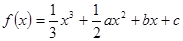 在
在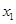 处取得极大值,在
处取得极大值,在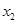 处取得极小值,满足
处取得极小值,满足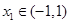 ,
,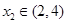 ,则
,则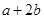 的取值范围是
的取值范围是
A.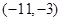 | B.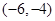 | C.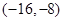 | D.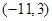 |
D
解析试题分析:解:∵函数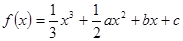 在x1处取得极大值,在x2处取得极小值,∴x1,x2是导函数f′(x)=x2+ax+b的两根,由于导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(-1,1),x2∈(2,4),则f′(-1)=1-a+b>0, f′(2)=4+2a+b<0, f′(4)=16+4a+b>0满足条件的约束条件的可行域如下图所示:令Z=2a+b,则ZA=3,ZB=-6,ZC=-11,故2a+b的取值范围是(-11,3)故选D
在x1处取得极大值,在x2处取得极小值,∴x1,x2是导函数f′(x)=x2+ax+b的两根,由于导函数f′(x)=x2+ax+b的图象开口朝上且x1∈(-1,1),x2∈(2,4),则f′(-1)=1-a+b>0, f′(2)=4+2a+b<0, f′(4)=16+4a+b>0满足条件的约束条件的可行域如下图所示:令Z=2a+b,则ZA=3,ZB=-6,ZC=-11,故2a+b的取值范围是(-11,3)故选D
考点:导数研究函数极值
点评:本题考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力,解题时要认真审题,仔细解答

练习册系列答案
相关题目
如图是函数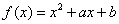 的部分图象,则函数
的部分图象,则函数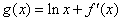 的零点所在的区间是( )
的零点所在的区间是( )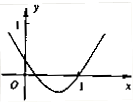
A. | B.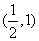 | C.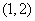 | D.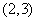 |
函数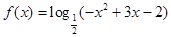 的单调递减区间为
的单调递减区间为
A.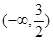 | B.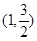 | C.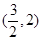 | D. |
函数 的零点所在的一个区间是( )
的零点所在的一个区间是( )
A. | B.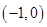 | C.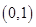 | D. |
用二分法计算函数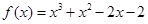 的一个正数零点的近似值(精确到0.1)为( )
的一个正数零点的近似值(精确到0.1)为( )
参考数据:
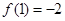 | 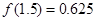 |
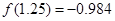 | 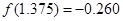 |
 | 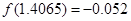 |
已知函数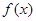 的导函数为
的导函数为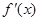 ,且满足
,且满足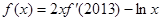 ,则
,则 ( )
( )
A.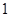 | B. | C. | D.无法确定 |
已知 是函数
是函数 的零点,若
的零点,若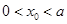 ,则
,则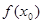 的值满足( )
的值满足( )
A.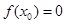 | B.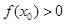 |
C.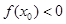 | D.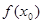 的符号不确定 的符号不确定 |
已知R上的函数y=f(x),其周期为2,且x∈(-1,1]时f(x)=1+x2,函数g(x)=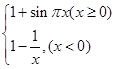 ,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
| A.11 | B.10 | C.9 | D.8 |
已知函数 ,则函数
,则函数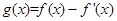 的零点所在的区间是( )
的零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |