题目内容
12.已知f(x)=|x-1|-|x+3|.(1)解不等式f(x)≤2;
(2)若f(x)-a≥0恒成立,求a的取值范围.
(3)若f(x)-a≥0有解,求a的取值范围.
分析 (1)由条件利用绝对值的意义求得不等式f(x)≤2的解集.
(2)由题意根据f(x)的最小值为-4,可得-4-a≥0,由此求得a的范围.
(3)由题意根据f(x)的最大值为4,可得4-a≥0,由此求得a的范围.
解答 解:(1)函数f(x)=|x-1|-|x+3|表示数轴上的x对应点到1对应点的距离减去它到-3对应点的距离,
而-2对应点到1对应点的距离减去它到-3对应点的距离正好等于2,
故不等式f(x)≤2的解集为{x|x≤2}.
(2)若f(x)-a≥0恒成立,由于f(x)的最小值为-4,故有-4-a≥0,∴a≤-4.
(3)若f(x)-a≥0有解,由于f(x)的最大值为4,故有4-a≥0,求得a≤4.
点评 本题主要考查绝对值的意义,函数的恒成立问题、函数的能成立问题,解绝对值不等式,求函数的最值,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下面是高考第一批录取的一份志愿表:
现有4所重点院校,每所院校有3个专业是你较为满意的选择,如果从中任选3所随意填报,表格填满且规定学校没有重复,同一学校的专业也没有重复的话,不同的填写方法的种数是多少?
| 志愿 | 第一志愿 | 第二志愿 | 第三志愿 |
| 学校 | 1 | 2 | 3 |
| 专业 | 第1专业 | 第1专业 | 第1专业 |
| 第2专业 | 第2专业 | 第2专业 |
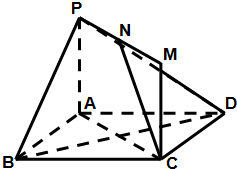 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,