题目内容
在自然数集N上定义一个函数y = f (x),已知f (1) + f (2)=5.当x为奇数时,f (x+1)-f (x)=1,当x为偶数时f (x+1)-f (x)=3.
(1)求证:f (1),f (3),f (5),……,f (2n-1) (n∈N+)成等差数列.
(2)求f (x)的解析式.
(1)求证:f (1),f (3),f (5),……,f (2n-1) (n∈N+)成等差数列.
(2)求f (x)的解析式.
(1)见解析;(2)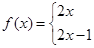 .
.
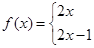 .
.(1)先构造关于f(1),f(2)的方程,然后根据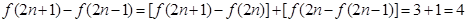 ,即可得证.
,即可得证.
(2)讨论x奇数和偶数,分别利用给的两个递推关系即可求出解析式.
解:(1)有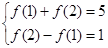
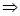
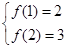
∴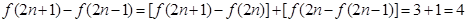
∴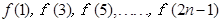 是首项为2,公差为4的等差数列
是首项为2,公差为4的等差数列
(2)当x为奇数时,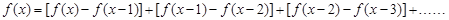
+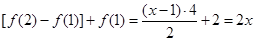
当x为偶数时,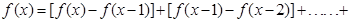
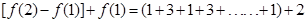
=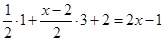
∴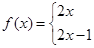 7’
7’
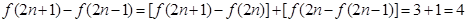 ,即可得证.
,即可得证.(2)讨论x奇数和偶数,分别利用给的两个递推关系即可求出解析式.
解:(1)有
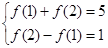
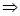
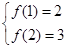
∴
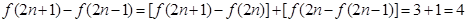
∴
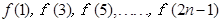 是首项为2,公差为4的等差数列
是首项为2,公差为4的等差数列(2)当x为奇数时,
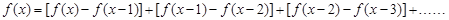
+
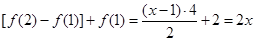
当x为偶数时,
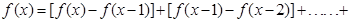
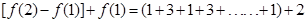
=
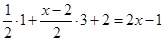
∴
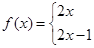 7’
7’
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ∥
∥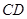 ,
,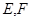 是线段
是线段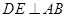 ,
,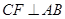 ,
,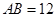 ,
,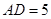 ,
,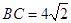 ,
,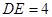 .现将△
.现将△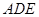 ,△
,△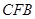 分别沿
分别沿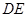 ,
,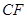 折起,使两点
折起,使两点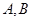 重合于点
重合于点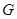 ,得到多面体
,得到多面体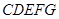 (1)求证:平面
(1)求证:平面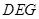
 平面
平面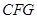 ;(2)求多面体
;(2)求多面体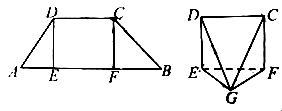
 为定义在R上的奇函数,当
为定义在R上的奇函数,当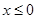 时,
时, (
(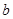 为常数),则
为常数),则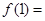
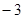
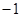
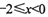 时,
时,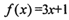 ,则f(5)的值为
,则f(5)的值为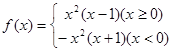 ,判断它的奇偶性。
,判断它的奇偶性。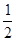 )|x|
)|x|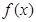 ,设其导函数
,设其导函数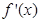 ,当
,当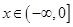 时,恒有
时,恒有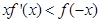 ,令
,令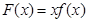 ,则满足
,则满足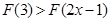 的实数x的取值范围是( )
的实数x的取值范围是( )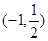
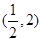
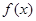 的定义域为
的定义域为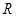 ,若存在常数
,若存在常数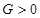 使
使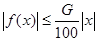 对一切实数
对一切实数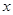 均成立,则称函数
均成立,则称函数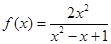 , ②
, ②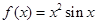 , ③
, ③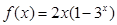 ,
,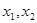 ,恒有
,恒有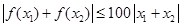 .
.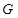 函数的序号为 ▲
函数的序号为 ▲ 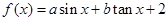 ,满足
,满足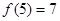 ,则
,则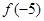 的值为( )
的值为( )