题目内容
设函数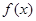 的定义域为
的定义域为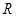 ,若存在常数
,若存在常数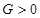 使
使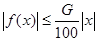 对一切实数
对一切实数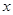 均成立,则称函数
均成立,则称函数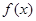 为G函数.现给出下列函数:
为G函数.现给出下列函数:
①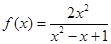 , ②
, ②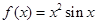 , ③
, ③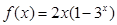 ,
,
④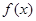 是定义在
是定义在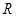 的奇函数,且对一切
的奇函数,且对一切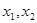 ,恒有
,恒有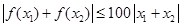 .
.
则其中是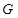 函数的序号为 ▲
函数的序号为 ▲
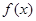 的定义域为
的定义域为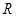 ,若存在常数
,若存在常数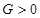 使
使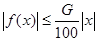 对一切实数
对一切实数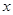 均成立,则称函数
均成立,则称函数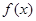 为G函数.现给出下列函数:
为G函数.现给出下列函数:①
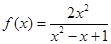 , ②
, ②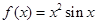 , ③
, ③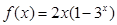 ,
,④
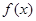 是定义在
是定义在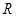 的奇函数,且对一切
的奇函数,且对一切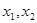 ,恒有
,恒有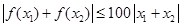 .
.则其中是
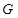 函数的序号为 ▲
函数的序号为 ▲ ①④
①当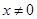 时,
时,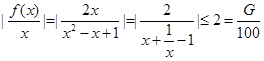 ;
;
②当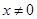 时,
时,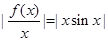 ,不存在常数
,不存在常数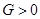 ,满足条件;
,满足条件;
③当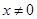 时,
时,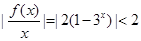 ,不存在常数
,不存在常数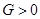 ,满足条件;
,满足条件;
④当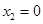 时,因为
时,因为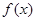 是定义在R上的奇函数,所以
是定义在R上的奇函数,所以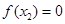 ,此时
,此时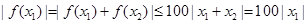 ,符合。
,符合。
综上可得,是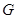 的为①④
的为①④
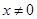 时,
时,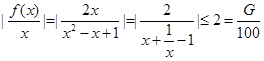 ;
;②当
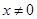 时,
时,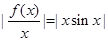 ,不存在常数
,不存在常数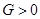 ,满足条件;
,满足条件;③当
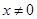 时,
时,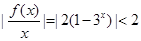 ,不存在常数
,不存在常数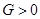 ,满足条件;
,满足条件;④当
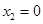 时,因为
时,因为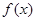 是定义在R上的奇函数,所以
是定义在R上的奇函数,所以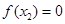 ,此时
,此时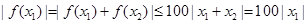 ,符合。
,符合。综上可得,是
 的为①④
的为①④
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的函数
的函数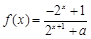 是奇函数,则
是奇函数,则 ▲ .
▲ .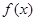 满足
满足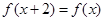 ,且当
,且当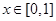 时,
时,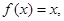 则函数
则函数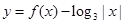 的零点个数是
的零点个数是 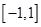 上的偶函数
上的偶函数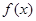 ,已知当
,已知当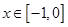 时的解析式
时的解析式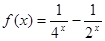
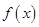 在
在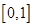 上的解析式;
上的解析式;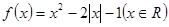 为 ▲ 函数.(填“奇”或“偶”)
为 ▲ 函数.(填“奇”或“偶”)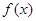 是
是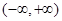 上的偶函数,若对于
上的偶函数,若对于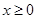 ,都有
,都有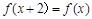 ,且当
,且当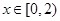 时,
时,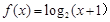 ,则
,则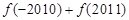 的值为 ( )
的值为 ( )

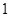

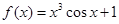 ,若
,若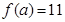 ,则
,则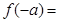 _______。
_______。