题目内容
19．若f（x）=x2+bx+c对任意实数x都有f（a+x）=f（a-x），则（ ）| A． | f（a）＜f（a-1）＜f（a+2） | B． | f（a-1）＜f（a）＜f（a+2） | C． | f（a）＜f（a+2）＜f（a-1） | D． | f（a+2）＜f（a）＜f（a-1） |
分析 根据已知分析出函数的图象和性质，进而可得三个函数值的大小．
解答 解：∵f（x）=x2+bx+c对任意实数x都有f（a+x）=f（a-x），
故函数f（x）的图象是开口朝上，且以直线x=a为对称轴的抛物线，
∴距离对称轴越近，函数值越小，
故f（a）＜f（a-1）＜f（a+2），
故选：A．
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
14．下列函数中，既是偶函数又在（-∞，0）单调递减的函数是（ ）
| A． | y=x3 | B． | y=|x|+1 | C． | y=-x2+1 | D． | y=2-|x| |
11．
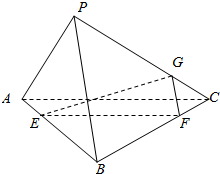如图，P是△ABC所在平面外一点，E，F，G分别在AB，BC，PC上，且PG=2GC，AC∥平面EFG，PB∥平面EFG．则$\frac{AE}{EB}$=（ ）
如图，P是△ABC所在平面外一点，E，F，G分别在AB，BC，PC上，且PG=2GC，AC∥平面EFG，PB∥平面EFG．则$\frac{AE}{EB}$=（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |