题目内容
9.在锐角△ABC中,三内角A,B,C的对边分别为a,b,c,若$A>B,cosA=\frac{1}{3}$,a+b=5,c=3.(Ⅰ)求a,b的值;
(Ⅱ)求cos(A+B)的值.
分析 (Ⅰ)由余弦定理得和题意可得a、b的方程组,解方程组可得;
(Ⅱ)由前面解答可得C=A,整体由诱导公式可得.
解答 解:(Ⅰ)在锐角△ABC中,由余弦定理得a2=b2+c2-2bccosA,
代入数据可得(5-b)2=b2+9-2b,
解得b=2,∴a=3;
(Ⅱ)∵a=c=3,∴C=A,
∴$cos(A+B)=cos(π-C)=-cosC=-cosA=-\frac{1}{3}$
点评 本题考查解三角形,涉及余弦定理的应用,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.点P(1,2,3)到原点的距离是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2 |
20.20152015除以8的余数为( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
18.下列函数中,既在定义域上是增函数且图象又关于原点对称的是( )
| A. | y=-$\frac{2}{x}$ | B. | y=lg($\frac{2}{1+x}$-1) | C. | y=2x | D. | y=2x+2-x |
19.若f(x)=x2+bx+c对任意实数x都有f(a+x)=f(a-x),则( )
| A. | f(a)<f(a-1)<f(a+2) | B. | f(a-1)<f(a)<f(a+2) | C. | f(a)<f(a+2)<f(a-1) | D. | f(a+2)<f(a)<f(a-1) |
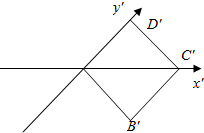 如图,A′B′C′D′是边长为1的正方形,又知它是某个四边形按斜二测画法画出的直观图,请画出该四边形的原图形,并求出原图形面积.
如图,A′B′C′D′是边长为1的正方形,又知它是某个四边形按斜二测画法画出的直观图,请画出该四边形的原图形,并求出原图形面积.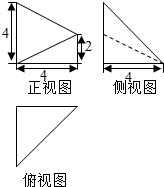 已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.将直角三角形△ABD绕斜边AD旋转一周,则BD=2;该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$.
已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.将直角三角形△ABD绕斜边AD旋转一周,则BD=2;该旋转体的表面积为$\frac{32+8\sqrt{2}}{3}π$.