题目内容
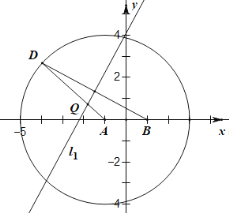
【题目】如图,已知圆![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,点
内一个定点,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() .当点
.当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为椭圆
的轨迹为椭圆![]() .
.
(1)![]() 分别为椭圆
分别为椭圆![]() 的左右焦点,
的左右焦点,![]() 为椭圆上任意一点,若
为椭圆上任意一点,若![]() ,求
,求![]() 的面积;
的面积;
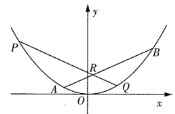
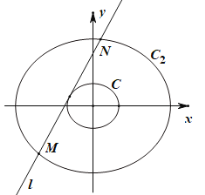
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() (
(![]() ,且
,且![]() ),则称椭圆
),则称椭圆![]() 是椭圆
是椭圆![]() 的
的![]() 倍相似椭圆.已知
倍相似椭圆.已知![]() 是椭圆
是椭圆![]() 的
的![]() 倍相似椭圆,若椭圆
倍相似椭圆,若椭圆![]() 的任意一条切线
的任意一条切线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() 、
、![]() ,试求弦长
,试求弦长![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
(1)根据线段中垂线的性质,可求出![]() 的方程为
的方程为![]() ,由椭圆的定义可知
,由椭圆的定义可知![]() ,结合已知条件可求出
,结合已知条件可求出![]() ,又
,又![]() ,结合余弦定理以及同角三角函数的基本关系可求出
,结合余弦定理以及同角三角函数的基本关系可求出![]() ,进而可求出三角形的面积.
,进而可求出三角形的面积.
(2)当切线斜率不存在时,可求出![]() ;若斜率存在,设方程为
;若斜率存在,设方程为![]() ,与
,与![]() 联立可知
联立可知![]() ,即
,即![]() ;与
;与![]() 联立,结合韦达定理、弦长公式可求出
联立,结合韦达定理、弦长公式可求出![]() ,从而可求出弦长
,从而可求出弦长![]() 的取值范围.
的取值范围.
(1)解:由题意知,圆心![]() ,半径
,半径![]() ,且
,且![]() ,
,
设椭圆的方程为![]() ,焦点坐标为
,焦点坐标为![]() ,由椭圆的定义可知,
,由椭圆的定义可知,![]() ,
,
解得![]() ,所以
,所以![]() ,所以
,所以![]() 的方程为
的方程为![]() .
.
因为![]() 为椭圆上任意一点,所以
为椭圆上任意一点,所以![]() ,由
,由![]() ,可知
,可知
![]() ,又因为
,又因为![]() ,由余弦定理知,
,由余弦定理知,
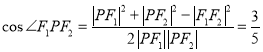 ,所以
,所以![]() ,
,
则![]() 的面积为
的面积为![]() .
.
(2)由(1)知,![]() 的方程为
的方程为![]() ,即
,即![]() .设
.设![]() .
.
①若切线垂直于![]() 轴,其方程为
轴,其方程为![]() ,不妨设为
,不妨设为![]() ,则
,则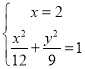 ,解得
,解得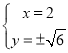 ,
,
所以此时,![]() ;同理对于切线为
;同理对于切线为![]() 时,求出
时,求出![]() .
.
②若切线不垂直于![]() 轴,设其方程为
轴,设其方程为![]() ,
,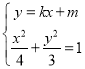 ,整理得
,整理得
![]() ,则
,则![]() ,即
,即![]() (
(![]() );
);
切线与![]() 联立得
联立得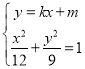 ,整理得
,整理得![]() ,
,
所以![]() ,则
,则![]()
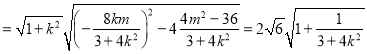 .
.
因为![]() ,所以
,所以![]() ,从而
,从而![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目