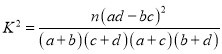题目内容
【题目】已知函数
，
.
（1）当
时，求
的单调区间；
（2）当
时，记函数
，若函数
至少有三个零点，求实数
的取值范围
【答案】（1）单调递增区间为
，
；单调递减区间为
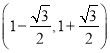；（2）
【解析】
（1）求导后，根据导函数的正负可确定函数的单调区间；
（2）求得导函数的零点后，分别在
、
和
三种情况下，根据函数的单调性和最值确定零点的个数，进而得到
的范围.
（1）令
，则当
时，
，
，令
，解得：
，
当
和时，
；当
时，
；
的单调递增区间为，；单调递减区间为；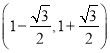
（2）当
时，
，
令
，解得：
，
，
①当，即
时，
，
此时
至多有两个零点，不合题意；
②当，即
时，
，此时至多有两个零点，不合题意；
③当，即
时，
（i）当
时，至多有两个零点，不合题意；
（ⅱ）当
时，
，
，
此时恰好有
个零点；
（iii）当
时，
，
，
，
记
，则
，
，
此时有四个零点；
综上所述：满足条件的实数的取值集合为.
【题目】2019年末，武汉出现新型冠状病毒（
肺炎疫情，并快速席卷我国其他地区，传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株，目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早，感染人员最多，防控压力最大，武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员，强化网格化管理，不落一户、不漏一人.在排查期间，某社区将本社区的排查工作人员分为
，
两个小组，排查工作期间社区随机抽取了100户已排查户，进行了对排查工作态度是否满意的电话调查，根据调查结果统计后，得到如下
的列联表.
是否满意 组别 | 不满意 | 满意 | 合计 |
| 16 | 34 | 50 |
| 2 | 45 | 50 |
合计 | 21 | 79 | 100 |
（1）分别估计社区居民对组、组两个排查组的工作态度满意的概率；
（2）根据列联表的数据，能否有
的把握认为“对社区排查工作态度满意”与“排查工作组别”有关？
附表：
|
|
|
|
|
|
|
|
|
|
|
|
附：
