题目内容
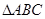 的周长是8,
的周长是8,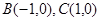 ,则顶点A的轨迹方程是( )
,则顶点A的轨迹方程是( ) A.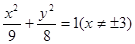 | B.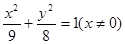 |
C.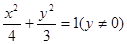 | D.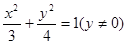 |
A
本题考查椭圆的定义,注意椭圆的定义中要检验两个线段的大小,看能不能构成椭圆,本题是一个易错题,容易忽略掉不合题意的点.
因为△ABC的两顶点B(-1,0),C(1,0),周长为8,∴BC=2,AB+AC=6,∵6>2,∴点A到两个定点的距离之和等于定值,根据椭圆的定义可知∴点A的轨迹是以B,C为焦点的椭圆,,∵2a=8,2c=4,所以椭圆的标准方程是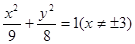 ,故选A.
,故选A.
解决该试题的关键是根据三角形的周长和定点,得到点A到两个定点的距离之和等于定值,得到点A的轨迹是椭圆,椭圆的焦点在y轴上,写出椭圆的方程,去掉不合题意的点。
因为△ABC的两顶点B(-1,0),C(1,0),周长为8,∴BC=2,AB+AC=6,∵6>2,∴点A到两个定点的距离之和等于定值,根据椭圆的定义可知∴点A的轨迹是以B,C为焦点的椭圆,,∵2a=8,2c=4,所以椭圆的标准方程是
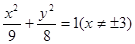 ,故选A.
,故选A.解决该试题的关键是根据三角形的周长和定点,得到点A到两个定点的距离之和等于定值,得到点A的轨迹是椭圆,椭圆的焦点在y轴上,写出椭圆的方程,去掉不合题意的点。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
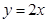 ,焦距为
,焦距为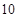 ,这双曲线的方程为___
,这双曲线的方程为___  内有一动点
内有一动点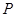 ,已知
,已知 ,且满足
,且满足 ,求
,求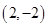 且与双曲线
且与双曲线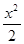 -y
-y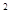 =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )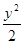 -
-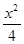 =1
=1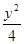 =1
=1 ,
, 为抛物线上一点,
为抛物线上一点, 为
为 关于
关于 轴对称的点,
轴对称的点, 为坐标原点.(1)若
为坐标原点.(1)若 ,求
,求 交抛物线
交抛物线 于
于 两点, 且斜率分别为
两点, 且斜率分别为 ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.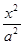 -
-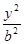 =1(
=1(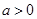 ,
,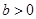 )的一个焦点,如果抛物线与双曲线交于
)的一个焦点,如果抛物线与双曲线交于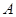 (
(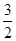 ,
,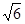 ),
),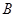 (
(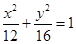 有公共焦点,且离心率互为倒数的双曲线的方程是
有公共焦点,且离心率互为倒数的双曲线的方程是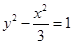
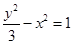

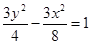
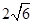 ).
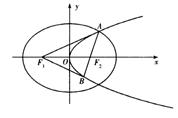
).
 、
、 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则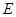 的离心率为( )
的离心率为( )


