题目内容
11.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{7}$,则<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.分析 由条件求得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,从而求得<$\overrightarrow{a}$,$\overrightarrow{b}$>的值.
解答 解:已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{7}$,∴${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=4-2×2×3cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+9=7,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,∴<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查两个向量的数量积的定义,根据三角函数的值求角,属于基础题.

练习册系列答案
相关题目
1.甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一,乙不值周六,则可排出不同的值班表数为( )
| A. | 6 | B. | 12 | C. | 42 | D. | 90 |
2.设P为△ABC内一点,且$\overrightarrow{AP}=\frac{3}{7}\overrightarrow{AB}+\frac{2}{7}\overrightarrow{AC}$,则△ABP与△ACP的面积之比为( )
| A. | 3:2 | B. | 2:3 | C. | 3:7 | D. | 7:2 |
19.不等式2kx2+kx-$\frac{3}{8}$<0对任何实数x恒成立,则k的取值范围是( )
| A. | (-3,0] | B. | (-3,0) | C. | [-3,0] | D. | [-3,0) |
6.在△ABC中,内角A,B,C的对边分别为a、b、c,且a、b、c成等比数列,a+c=3,tanB=$\frac{{\sqrt{7}}}{3}$,则△ABC的面积为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
20.设实数x,y满足:$\left\{\begin{array}{l}{2x+y≤4}\\{x-2y≤2}\\{x-y≥1}\end{array}\right.$,O为坐标原点,则x2+y2的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
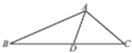 如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.
如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.