题目内容
已知以点
为圆心的圆与直线
相切，过点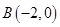
的动直线与圆
相交于
两点.
（1）求圆的方程；
（2）当
时，求直线
的方程.
（1）
；（2）
或
.
解析试题分析：（1）由直线与以为圆心的圆相切得到该圆的半径，然后根据圆心的坐标与半径即可写出圆的标准方程；（2）先由弦
的长与圆的半径得到圆心到直线的距离
，进而设出直线的方程
（注意检验直线斜率不存在的情况），由点到直线的距离公式即可算出
的取值，从而可写出直线的方程.
试题解析：（1）由题意知到直线
的距离为圆半径
圆的方程为
（2）设线段的中点为
，连结
，则由垂径定理可知
，且
，在
中由勾股定理易知
当动直线的斜率不存在时，直线的方程为时，显然满足题意；
当动直线的斜率存在时，设动直线的方程为：
由到动直线的距离为1得
或为所求方程.
考点：1.圆的标准方程；2.点到直线的距离公式；3.直线与圆的位置关系.
练习册系列答案
相关题目
相切
被圆C所截得的弦AB的长．
和
，且圆心C在直线
：
上，求圆心为Ｃ的圆的标准方程．
是椭圆
上两点，点M的坐标为
.
轴对称，且
为等边三角形时，求
的长；
轴正半轴为极轴，已知点P的直角坐标为(1,-5),点C的极坐标为
,若直线l经过点P,且倾斜角为
，圆C的半径为4.
：
，点
，直线
.
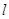垂直的直线方程；
上（
为坐标原点），存在定点
（不同于点
），满足：对于圆
，都有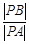
为一常数，试求出所有满足条件的点
时，求直线l的方程；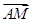
·
是否与直线l的倾斜角有关？若无关，请求出其值；若有关，请说明理由．
内有一点
，
为过点
且倾斜角为
的弦．
时，求
；
，求点
的方程为
,直线
的方程为
,点
在直线
,切点为
.
,试求点
点的坐标为
,过
两点,当
时,求直线
的方程;