题目内容
已知 是椭圆
是椭圆 上两点,点M的坐标为
上两点,点M的坐标为 .
.
(1)当 两点关于
两点关于 轴对称,且
轴对称,且 为等边三角形时,求
为等边三角形时,求 的长;
的长;
(2)当 两点不关于
两点不关于 轴对称时,证明:
轴对称时,证明: 不可能为等边三角形.
不可能为等边三角形.
(1) 或
或 ,(2)详见解析.
,(2)详见解析.
解析试题分析:(1)求 的长,实际求出
的长,实际求出 坐标.利用正三角形性质列等量关系.设
坐标.利用正三角形性质列等量关系.设 ,
, ,则
,则 .又点
.又点 在椭圆上,所以
在椭圆上,所以 解得
解得 或
或 ,
, 或
或 ,(2)本题实际应用逆否命题与原命题等价进行解题,即当
,(2)本题实际应用逆否命题与原命题等价进行解题,即当 为等边三角形时,
为等边三角形时, 两点必关于
两点必关于 轴对称,即横坐标相等.设
轴对称,即横坐标相等.设 ,则由
,则由 ,可化简
,可化简 ,同理可得
,同理可得 ,而
,而 ,因此
,因此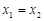 或
或 又
又 所以
所以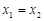 .
.
试题解析:解:
(1)设 ,
, , 1分
, 1分
因为 为等边三角形,所以
为等边三角形,所以 . 2分
. 2分
又点 在椭圆上,
在椭圆上,
所以 消去
消去 , 3分
, 3分
得到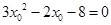 ,解得
,解得 或
或 , 4分
, 4分
当 时,
时, ;
;
当 时,
时, . 5分
. 5分
{说明:若少一种情况扣2分}
(2)法1:根据题意可知,直线 斜率存在.
斜率存在.
设直线 :
: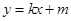 ,
, ,
, ,
, 中点为
中点为 ,
,
联立 消去
消去 得
得 , 6分
, 6分
由 得到
得到 ① 7分
① 7分
所以 ,
, , 8分
, 8分
所以 ,又
,又
如果 为等边三角形,则有
为等边三角形,则有 , 9分
, 9分
所以 ,即
,即 , 10分
, 10分
化简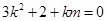 ,② 11分
,② 11分
由②得 ,代入①得
,代入①得 ,
,
化简得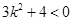 ,不成立,
,不成立,

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 关于直线
关于直线 对称,圆心
对称,圆心 在第二象限,半径为
在第二象限,半径为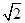 .
. 与圆
与圆 轴、
轴、 轴上的截距相等?若存在,求直线的方程;若不存在,说明理由.
轴上的截距相等?若存在,求直线的方程;若不存在,说明理由. 是直线
是直线
 上一动点,
上一动点,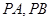 是圆C:
是圆C: 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形 的最小面积是2,则
的最小面积是2,则 的值为?
的值为? 中,以O为圆心的圆与直线
中,以O为圆心的圆与直线 相切.
相切. 轴相交于
轴相交于 两点,圆内的动点
两点,圆内的动点 满足
满足 ,
, 的取值范围.
的取值范围. 中,如图,已知椭圆E:
中,如图,已知椭圆E: 的左、右顶点分别为
的左、右顶点分别为 、
、 ,上、下顶点分别为
,上、下顶点分别为 、
、 .设直线
.设直线 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆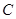 与以线段
与以线段 为直径的圆关于直线
为直径的圆关于直线
 ,求圆
,求圆 轴所得弦长为
轴所得弦长为 ;②被
;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为 ;③圆心到直线
;③圆心到直线 :
: 的距离为
的距离为 的圆的方程。
的圆的方程。 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点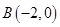 的动直线与圆
的动直线与圆 相交于
相交于 两点.
两点. 时,求直线
时,求直线 的方程.
的方程. (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点. (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.