题目内容
(本小题满分10分)选修4-1:几何证明选讲.
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
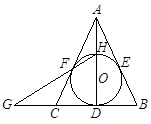
⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
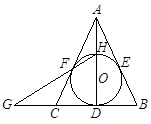
⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.
见解析。
切线PA和PB,切点分别是A和B根据切线的性质和圆周角定理,四边形内角和是360度即可求得劣弧AB的度数.
证明⑴:∵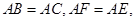 ∴
∴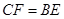 .
.
又∵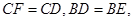 ∴
∴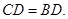
又∵△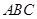 是等腰三角形,
是等腰三角形,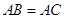 ,∴
,∴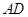 是角∠
是角∠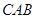 的平分线.
的平分线.
∴内切圆圆心O在直线AD上. (5分)
⑵连接DF,由⑴知,DH是⊙O的直径,

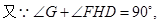
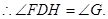
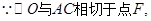
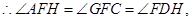
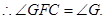
 ∴点C是线段GD的中点. (10分)
∴点C是线段GD的中点. (10分)
证明⑴:∵
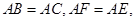 ∴
∴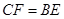 .
.又∵
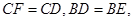 ∴
∴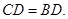
又∵△
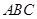 是等腰三角形,
是等腰三角形,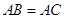 ,∴
,∴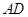 是角∠
是角∠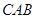 的平分线.
的平分线.∴内切圆圆心O在直线AD上. (5分)
⑵连接DF,由⑴知,DH是⊙O的直径,

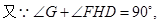
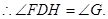
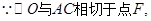
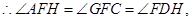
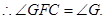
 ∴点C是线段GD的中点. (10分)
∴点C是线段GD的中点. (10分)
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
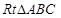 中,
中,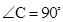 ,
,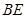 平分
平分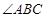 交
交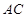 于点
于点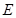 ,点
,点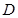 在
在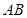 上,
上,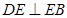 .
.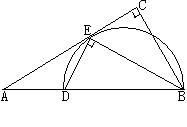
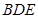 的外接圆的切线;
的外接圆的切线;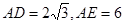 ,求
,求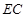 的长.
的长. 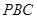 经过圆心O,
经过圆心O,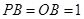 ,
,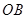 绕点
绕点 逆时针旋120°到
逆时针旋120°到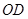 ,连
,连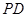 交圆
交圆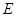 ,则
,则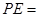 。
。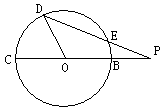
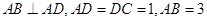 , 动点P在以点C为圆心,且与直线BD相切的圆内运动,设
, 动点P在以点C为圆心,且与直线BD相切的圆内运动,设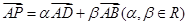 ,则α+β的取值范围是 ( )
,则α+β的取值范围是 ( )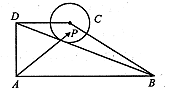
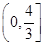
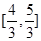
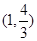
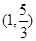
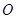 上一点
上一点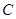 在直径
在直径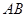 上的射影为
上的射影为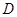 .
.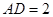 ,
,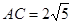 ,则
,则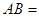 .
.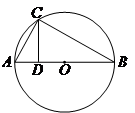
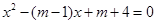 的两根,
的两根,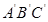 与△ABC开始时完全重合,然后让△ABC固定不动,将
与△ABC开始时完全重合,然后让△ABC固定不动,将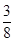 平方厘米?
平方厘米?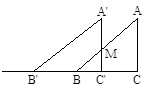
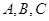 是圆
是圆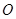 上的点,
上的点,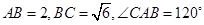 ,则
,则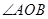 对应的劣弧长为 .
对应的劣弧长为 .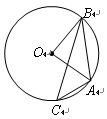
 和18
和18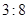 ,则另一弦的
,则另一弦的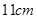
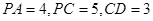 ,则
,则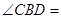 ( )
( )